
【题目】已知函数![]() 。
。
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() 对定义域内的任意
对定义域内的任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
【答案】(1)当![]() 时函数
时函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增.(2)
上单调递增.(2)![]() .
.
【解析】
试题分析:(1)求导得![]() ,分
,分![]() 分别讨论导函数的符号即可得到函数的单调性;(2)
分别讨论导函数的符号即可得到函数的单调性;(2) ![]() 对定义域内的任意
对定义域内的任意![]() 恒成立
恒成立![]() ,由(1)分别求函数的最小值,求解即可.
,由(1)分别求函数的最小值,求解即可.
试题解析: (1)求导可得![]()
①![]() 时,令
时,令![]() 可得
可得![]() ,由于
,由于![]() 知
知![]() ;令
;令![]() ,得
,得![]()
∴函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
②![]() 时,令
时,令![]() 可得
可得![]() ;令
;令![]() ,得
,得![]() 或
或![]() ,由于
,由于![]() 知
知![]() 或
或![]()
∴函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增
上单调递增
③![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增
上单调递增
④![]() 时,令
时,令![]() 可得
可得![]() ;令
;令![]() ,得
,得![]() 或
或![]() ,由于
,由于![]() 知
知![]() 或
或![]()
∴函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增
上单调递增
(2)![]() 时,
时,![]() ,舍去
,舍去
![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,故函数在
上单调递增,故函数在![]() 处取得最小值,所以函数
处取得最小值,所以函数![]() 对定义域内的任意
对定义域内的任意![]() 恒成立时,只需要
恒成立时,只需要![]() 即可
即可
∴![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是实数,
是实数,![]() ,
,
(1)若函数![]() 为奇函数,求
为奇函数,求![]() 的值;
的值;
(2)试用定义证明:对于任意![]() ,
,![]() 在
在![]() 上为单调递增函数;
上为单调递增函数;
(3)若函数![]() 为奇函数,且不等式
为奇函数,且不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某测观点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某企业原有员工1000人,每人每年可为企业创利润15万元,为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超过原有员工的2%,并且每年给每位待岗员工发放生活补贴1万元.据评估,当待岗员工人数![]() 不超过原有员工1.4%时,留岗员工每人每年可为企业多创利润
不超过原有员工1.4%时,留岗员工每人每年可为企业多创利润![]() 万元;当待岗员工人数
万元;当待岗员工人数![]() 超过原有员工1.4%时,留岗员工每人每年可为企业多创利润1.8万元.
超过原有员工1.4%时,留岗员工每人每年可为企业多创利润1.8万元.
(1)求企业年利润![]() (万元)关于待岗员工人数
(万元)关于待岗员工人数![]() 的函数关系式
的函数关系式![]() ;
;
(2)为使企业年利润最大,应安排多少员工待岗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点与两焦点构成的三角形为正三角形.
,上顶点与两焦点构成的三角形为正三角形.
(1)求椭圆![]() 的离心率;
的离心率;
(2)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,若
两点,若![]() 的内切圆的面积的最大值为
的内切圆的面积的最大值为![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B={抽到二等品},事件C={抽到三等品},且已知P(A)=0.65,P(B)=0.2,P(C)=0.1.则事件“抽到的是二等品或三等品”的概率为( )
A. 0.7 B. 0.65
C. 0.35 D. 0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC![]() A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.
A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.
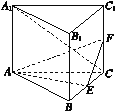
(Ⅰ)证明:平面AEF⊥平面B1BCC1;
(Ⅱ)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F![]() AEC的体积.
AEC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() ).
).
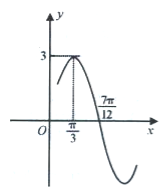
(1)若![]() 的部分图像如图所示,求
的部分图像如图所示,求![]() 的解析式;
的解析式;
(2)在(1)的条件下,求最小正实数![]() ,使得函数
,使得函数![]() 的图象向左平移
的图象向左平移![]() 个单位后所对应的函数是偶函数;
个单位后所对应的函数是偶函数;
(3)若![]() 在
在![]() 上是单调递增函数,求
上是单调递增函数,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com