
分析 (1)设等比数列{bn}的公比为q,则1+d=b1q,1+4d=${b}_{1}{q}^{2}$,1+13d=b1q3,d>0.联立解出即可得出.(2)数列{cn}对任意正整数n,均有$\frac{c_1}{b_1}+\frac{c_2}{b_2}+\frac{c_3}{b_3}+…+\frac{c_n}{b_n}={a_{n+1}}$,n=1时,$\frac{{c}_{1}}{{b}_{1}}$=a2,解得c1.n≥2时,$\frac{{c}_{1}}{{b}_{1}}+\frac{{c}_{2}}{{b}_{2}}$+…+$\frac{{c}_{n-1}}{{b}_{n-1}}$=an,相减可得$\frac{{c}_{n}}{{b}_{n}}$=d,可得cn=2×3n-1,再利用等比数列的求和公式即可得出.
解答 解:(1)设等比数列{bn}的公比为q,则1+d=b1q,1+4d=${b}_{1}{q}^{2}$,1+13d=b1q3,d>0.
联立解得:d=2,q=3,b1=1.
∴an=1+2(n-1)=2n-1.
bn=3n-1.
(2)数列{cn}对任意正整数n,均有$\frac{c_1}{b_1}+\frac{c_2}{b_2}+\frac{c_3}{b_3}+…+\frac{c_n}{b_n}={a_{n+1}}$,
n=1时,$\frac{{c}_{1}}{{b}_{1}}$=a2,解得c1=3.
n≥2时,$\frac{{c}_{1}}{{b}_{1}}+\frac{{c}_{2}}{{b}_{2}}$+…+$\frac{{c}_{n-1}}{{b}_{n-1}}$=an,
∴$\frac{{c}_{n}}{{b}_{n}}$=d,可得cn=2×3n-1,
∴c1+c2+c3+…+c2004=$2×\frac{{3}^{2004}-1}{3-1}$=32004-1.
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| 零件数(个) | 18 | 20 | 22 |
| 加工时间y(分钟) | 27 | 30 | 33 |
| A. | 84分钟 | B. | 94分钟 | C. | 102分钟 | D. | 112分钟 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的定义域关于原点对称是f(x)具有奇偶性的充分不必要条件 | |
| B. | 命题“若x≥4且y≥2,则x+y≥6”的逆否命题为“若x+y<6,则x<4且y<2” | |
| C. | 若p:?x≥0,x2-x+1>0,则¬p:?x<0,x2-x+1≤0 | |
| D. | 己知n∈N,则幂函数y=x3n-7为偶函数,且在x∈(0,+∞)上单调递减的充分必要条件为n=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
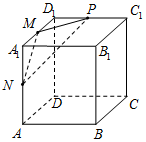 正方体ABCD-A1B1C1D1棱长为4,M,N,P分别是棱A1D1,A1A,D1C1的中点,则过M,N,P三点的平面截正方体所得截面的面积为( )
正方体ABCD-A1B1C1D1棱长为4,M,N,P分别是棱A1D1,A1A,D1C1的中点,则过M,N,P三点的平面截正方体所得截面的面积为( )| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | $12\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | [0,1) | C. | [0,3] | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com