练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．给出以下四个判断，其中正确的判断是（　　）
    A．函数f（x）的定义域关于原点对称是f（x）具有奇偶性的充分不必要条件
    B．命题“若x≥4且y≥2，则x+y≥6”的逆否命题为“若x+y＜6，则x＜4且y＜2”
    C．若p：?x≥0，x2-x+1＞0，则￢p：?x＜0，x2-x+1≤0
    D．己知n∈N，则幂函数y=x3n-7为偶函数，且在x∈（0，+∞）上单调递减的充分必要条件为n=1

    分析 A，是必要非充分条件；
    B，原命题的逆否命题为“若x+y＜6，则x＜4或y＜2”；
    C，若p：?x≥0，x2-x+1＞0，则￢p：?x≥0，x2-x+1≤0；
    D，幂函数y=x3n-7在x∈（0，+∞）上单调递减可得，n=0，1或2；又y=x3n-7为偶函数，可得n

    解答 解：对于 A，函数f（x）的定义域关于原点对称是f（x）具有奇偶性的必要非充分条件，故错；
    对于B，原命题的逆否命题为“若x+y＜6，则x＜4或y＜2”，故错；
    对于C，若p：?x≥0，x2-x+1＞0，则￢p：?x≥0，x2-x+1≤0故错；
    对于D，因为幂函数y=x3n-7在x∈（0，+∞）上单调递减，
    所以3n-7＜0，解得n＜$\frac{7}{3}$，又n∈N，
    所以，n=0，1或2；又y=x3n-7为偶函数，
    所以，n=1，即幂函数y=x3n-7为偶函数，且在x∈（0，+∞）上单调递减的充分必要条件为n=1，故正确；
    故选：D

    点评 本题考查了命题真假的判定，涉及到了充要条件、命题的否定、命题的四种形式等基础知识，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．（$\sqrt{x}$+3）（$\sqrt{x}$-$\frac{2}{x}$）5的展开式中的常数项为40．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知a＞0，b＞-1，且a+b=1，则$\frac{{a}^{2}+2}{a}$+$\frac{{b}^{2}}{b+1}$的最小值为$\frac{3+2\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．曲线y=xlnx在x=e处的切线方程为（　　）
    A．y=x-eB．y=2x-eC．y=xD．y=x+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

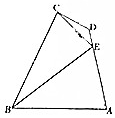    3．如图，在平面四边形ABCD中，DA⊥AB，CE⊥BE，DE=1，DC=2，AB=2$\sqrt{7}$，∠CDE=$\frac{2π}{3}$
    （Ⅰ）求sin∠CED的值及BC的长；
    （Ⅱ）求四边形ABCD的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．在△ABC中，已知cosA=$\frac{2\sqrt{5}}{5}$，C=$\frac{3π}{4}$，b=$\sqrt{2}$，若△ABC最大边的边长为$\sqrt{10}$，则△ABC的面积为1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．设A={x∈Z|-6≤x≤6}，B={1，2，3}，C={3，4，5，6}，求：（1）A∪（B∩C）；  （2）A∩∁A（B∩C）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知等差数列{an}的首项a1=1，公差d＞0，且第二项，第五项，第十四项分别是等比数列{bn}的第二项，第三项，第四项．
    （1）求数列{an}与{bn}的通项公式．
    （2）设数列{cn}对任意正整数n，均有$\frac{c_1}{b_1}+\frac{c_2}{b_2}+\frac{c_3}{b_3}+…+\frac{c_n}{b_n}={a_{n+1}}$，求c1+c2+c3+…+c2004的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．等差数列{an}的前n项和为Sn，若2a6+a7-a9=18，则S6-S3=（　　）
    A．18B．27C．36D．45

    查看答案和解析>>

    同步练习册答案