
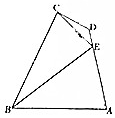
 如图,在平面四边形ABCD中,DA⊥AB,CE⊥BE,DE=1,DC=2,AB=2$\sqrt{7}$,∠CDE=$\frac{2π}{3}$
如图,在平面四边形ABCD中,DA⊥AB,CE⊥BE,DE=1,DC=2,AB=2$\sqrt{7}$,∠CDE=$\frac{2π}{3}$分析 (Ⅰ)由已知及余弦定理可求CE的值,进而利用正弦定理可求sin∠CED=$\frac{CD•sin∠CDE}{CE}$的值.
(Ⅱ)由∠CED+∠AEB=$\frac{π}{2}$,∠ABE+∠AEB=$\frac{π}{2}$,及(Ⅰ)可求sin∠ABE=$\frac{\sqrt{21}}{7}$,利用同角三角函数基本关系式可求cos∠ABE,在直角三角形△ABE中,可求BE,AE的值,进而利用三角形面积公式即可计算得解.
解答 解:(Ⅰ)∵DE=1,DC=2,∠CDE=$\frac{2π}{3}$,
∴由余弦定理可得:CE=$\sqrt{C{D}^{2}+D{E}^{2}-2CD•DE•cos∠CDE}$=$\sqrt{{2}^{2}+{1}^{2}-2×1×2×(-\frac{1}{2})}$=$\sqrt{7}$,
∴由正弦定理$\frac{CE}{sin∠CDE}=\frac{CD}{sin∠CED}$,可得:sin∠CED=$\frac{CD•sin∠CDE}{CE}$=$\frac{2×\frac{\sqrt{3}}{2}}{\sqrt{7}}$=$\frac{\sqrt{21}}{7}$.
(Ⅱ)∵∠CED+∠AEB=$\frac{π}{2}$,∠ABE+∠AEB=$\frac{π}{2}$,
∴sin∠ABE=sin∠CED=$\frac{\sqrt{21}}{7}$,cos∠ABE=$\sqrt{1-(\frac{\sqrt{21}}{7})^{2}}$=$\frac{2\sqrt{7}}{7}$,tan∠ABE=$\frac{\sqrt{3}}{2}$,
∵AB=2$\sqrt{7}$,
∴在△ABE中,由cos∠ABE=$\frac{AB}{BE}$,可得:BE=$\frac{AB}{cos∠ABE}$=$\frac{2\sqrt{7}}{\frac{2\sqrt{7}}{7}}$=7,AE=BE•sin∠ABE=7×$\frac{\sqrt{21}}{7}$=$\sqrt{21}$,
∴S四边形ABCD=S△CDE+S△CBE+SABE=$\frac{1}{2}DE•CD•sin∠CDE$+$\frac{1}{2}$BE•CE+$\frac{1}{2}AB•AE$=$\frac{1}{2}$×$1×2×\frac{\sqrt{3}}{2}$+$\frac{1}{2}×7×\sqrt{7}$+$\frac{1}{2}×2\sqrt{7}×\sqrt{21}$=$\frac{15\sqrt{3}+7\sqrt{7}}{2}$.
点评 本题主要考查了余弦定理,正弦定理,同角三角函数基本关系式,三角形面积公式在解三角形中的综合应用,考查了数形结合思想和转化思想的应用,属于中档题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:选择题
| A. | 若统计量X2>6.64,我们有99%的把握说吸烟与患肺癌有关,则某人吸烟,那么他有99%的可能患肺癌 | |
| B. | 若从统计中得出,有99%的把握说吸烟与患肺癌有关,则在100个吸烟者中必有99个人患有肺病 | |
| C. | 若从统计量中得出,有99%的把握说吸烟与患肺癌有关,是指有1%的可能性使得推断错误 | |
| D. | 以上说法均不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的定义域关于原点对称是f(x)具有奇偶性的充分不必要条件 | |
| B. | 命题“若x≥4且y≥2,则x+y≥6”的逆否命题为“若x+y<6,则x<4且y<2” | |
| C. | 若p:?x≥0,x2-x+1>0,则¬p:?x<0,x2-x+1≤0 | |
| D. | 己知n∈N,则幂函数y=x3n-7为偶函数,且在x∈(0,+∞)上单调递减的充分必要条件为n=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com