
 如图,在三棱锥A-BCD中,E是AC中点,F在AD上,且2AF=FD,若三棱锥A-BEF的体积是1,则四棱锥B-ECDF的体积为5.
如图,在三棱锥A-BCD中,E是AC中点,F在AD上,且2AF=FD,若三棱锥A-BEF的体积是1,则四棱锥B-ECDF的体积为5. 分析 设点B到平面ACD的距离为h,则VA-BEF=VB-AEF=$\frac{1}{3}×h×(\frac{1}{2}×AE×AF×sin∠EAF)$=1,从而VB-ACD=$\frac{1}{3}×h×{S}_{△ACD}$=$\frac{1}{3}×h×(\frac{1}{2}×2AE×3AF×sin∠EAF)$=6,四棱锥B-ECDF的体积V=VB-ACD-VA-AEF,由此能求出结果.
解答 解:设点B到平面ACD的距离为h,
∵在三棱锥A-BCD中,E是AC中点,F在AD上,且2AF=FD,三棱锥A-BEF的体积是1,
∴VA-BEF=VB-AEF=$\frac{1}{3}×h×{S}_{△AEF}$=$\frac{1}{3}×h×(\frac{1}{2}×AE×AF×sin∠EAF)$=1,
∴VB-ACD=$\frac{1}{3}×h×{S}_{△ACD}$=$\frac{1}{3}×h×(\frac{1}{2}×AC×AD×sin∠CAD)$
=$\frac{1}{3}×h×(\frac{1}{2}×2AE×3AF×sin∠EAF)$=6×[$\frac{1}{3}×h×(\frac{1}{2}×AE×AF×sin∠EAF)$]=6.
∴四棱锥B-ECDF的体积V=VB-ACD-VA-BEF=6-1=5.
故答案为:5.
点评 本题考查四棱锥的体积的求法,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{10}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
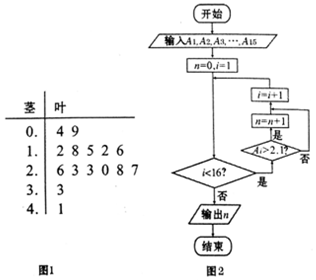 图1是随机抽取的15户居民月均用水量(单位:t)的茎叶图,月均用水量依次记为A1、A2、…A15,图2是统计茎叶图中月均用水量在一定范围内的频数的一个程序框图,那么输出的结果n=7.
图1是随机抽取的15户居民月均用水量(单位:t)的茎叶图,月均用水量依次记为A1、A2、…A15,图2是统计茎叶图中月均用水量在一定范围内的频数的一个程序框图,那么输出的结果n=7.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com