
分析 (1)由f(2)<f(3)知幂函数在(0,+∞)上为增函数,故(2-k)(1+k)>0,解出k即可.
(2)写出g(x)的解析式g(x)=-qx2+(2q-1)x+1,为二次函数,只需考虑二次函数的对称轴和单调性即可.
解答 解:(1)因为幂函数f(x)=x(2-k)(1-k) 在(0,+∞)上单调递增,
所以(2-k)(1+k)>0,故-1<k<2.
又因为k∈Z,故k=0,或k=1,所以f(x)=x2.
(2)由(1)知g(x)=-qx2+(2q-1)x+1,
假设存在这样的正数q符合题意,
则函数g(x)的图象是开口向下的抛物线,
其对称轴为x=$\frac{2q-1}{2q}$=1-$\frac{1}{2q}$<1,
因而,函数g(x)在[-1,2]上的最小值只能在x=-1或x=2处取得
又g(2)=-4q+4q-2+1=-1≠-4,从而必有g(-1)=2-3q=-4
解得q=2,
此时,g(x)=-2x2+3x+1,其对称轴x=$\frac{3}{4}$∈[-1,2]
∴g(x)在[-1,2]上的最大值为g($\frac{3}{4}$)=-2×($\frac{3}{4}$)2+3×$\frac{3}{4}$+1=$\frac{17}{8}$符合题意.
点评 本题考查幂函数的单调性、二次函数的值域问题,考查利用所学知识分析问题、解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 6 | C. | 9$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| ξ | 1 | 2 | 3 |
| P | 0.5 | x | y |
| A. | $\frac{55}{64}$ | B. | $\frac{33}{64}$ | C. | $\frac{7}{32}$ | D. | $\frac{9}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限角一定是锐角 | |
| B. | {α|α=kπ+$\frac{π}{6}$,k∈Z}≠{β|β=-kπ+$\frac{π}{6}$,k∈Z} | |
| C. | 若α是第二象限的角,则sin2α<0 | |
| D. | 第四象限的角可表示为{α|2kπ+$\frac{3}{2}$π<α<2kπ,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
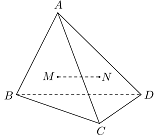 如图,A是△BCD所在平面外一点,M、N为△ABC和△ACD重心,BD=6;
如图,A是△BCD所在平面外一点,M、N为△ABC和△ACD重心,BD=6;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 7816 | 6572 | 0802 | 6314 | 0702 | 4369 | 9728 | 0198 |
| 3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
| A. | 63 | B. | 02 | C. | 43 | D. | 07 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com