
【题目】已知函数f(x)=lnx﹣x3与g(x)=x3﹣ax的图象上存在关于x轴的对称点,e为自然对数的底数,则实数a的取值范围是( )
A.(﹣∞,e)
B.(﹣∞,e]
C.(﹣∞, ![]() )
)
D.(﹣∞, ![]() ]
]
科目:高中数学 来源: 题型:
【题目】已知函数![]() (k
(k![]() R),且满足f(﹣1)=f(1).
R),且满足f(﹣1)=f(1).
(1)求k的值;
(2)若函数y=f(x)的图象与直线![]() 没有交点,求a的取值范围;
没有交点,求a的取值范围;
(3)若函数![]() ,x
,x![]() [0,log23],是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
[0,log23],是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李冶(1192﹣1279),真定栾城(今属河北石家庄市)人,金元时期的数学家、诗人、晚年在封龙山隐居讲学,数学著作多部,其中《益古演段》主要研究平面图形问题:求圆的直径,正方形的边长等,其中一问:现有正方形方田一块,内部有一个圆形水池,其中水池的边缘与方田四边之间的面积为13.75亩,若方田的四边到水池的最近距离均为二十步,则圆池直径和方田的边长分别是(注:240平方步为1亩,圆周率按3近似计算)( )
A.10步、50步
B.20步、60步
C.30步、70步
D.40步、80步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mln(x+1),g(x)= ![]() (x>﹣1).
(x>﹣1).
(Ⅰ)讨论函数F(x)=f(x)﹣g(x)在(﹣1,+∞)上的单调性;
(Ⅱ)若y=f(x)与y=g(x)的图象有且仅有一条公切线,试求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
已知函数f(x)=|a﹣x|(a∈R)
(Ⅰ)当a= ![]() 时,求使不等式f(2x﹣
时,求使不等式f(2x﹣ ![]() )>2f(x+2)+2成立的x的集合A;
)>2f(x+2)+2成立的x的集合A;
(Ⅱ)设x0∈A,证明f(x0x)≥x0f(x)+f(ax0).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表: 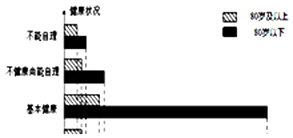
(1)若采取分层抽样的方法再从样本中的不能自理的老人中抽取16人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发 放生活补贴,标准如下:①80岁及以上长者每人每月发放生活补贴200元;②80岁以下 老人每人每月发放生活补贴120元;③不能自理的老人每人每月额外发放生活补贴100 元.试估计政府执行此计划的年度预算.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由实数组成的等比数列{an}的前项和为Sn , 且满足8a4=a7 , S7=254.
(1)求数列{an}的通项公式;
(2)对n∈N* , bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com