练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知，，且对恒成立，则的最大值是（ ）

    A. B. C. D.

    【答案】C

    【解析】分析：先求出函数的导数，再分别讨论a=0，a＜0，a＞0的情况，从而得出ab的最大值．

    详解：令f（x）=ex-a（x-1）-b，则f′（x）=ex-a，
    若a=0，则f（x）=ex-b≥-b≥0，得b≤0，此时ab=0；
    若a＜0，则f′（x）＞0，函数单调增，x→-∞，此时f（x）→-∞，不可能恒有f（x）≥0．
    若a＞0，由f′（x）=ex-a=0，得极小值点x=lna，
    由f（lna）=a-alna+a-b≥0，得b≤a（2-lna），ab≤a2（2-lna）．令g（a）=a2（2-lna）．则g′（a）=2a（2-lna）-a=a（3-2lna）=0，得极大值点a=．而g（）=∴ab的最大值是故选C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知点A(0，－2)，椭圆E： (a>b>0)的离心率为，F是椭圆E的右焦点，直线AF的斜率为，O为坐标原点.

    (1)求E的方程；

    (2)设过点A的动直线l与E相交于P，Q两点.当△OPQ的面积最大时，求l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若无穷数列满足：只要，必有，则称具有性质.

    （1）若具有性质，且， ，求；

    （2）若无穷数列是等差数列，无穷数列是公比为正数的等比数列， ， ， 判断是否具有性质，并说明理由；

    （3）设是无穷数列，已知.求证：“对任意都具有性质”的充要条件为“是常数列”.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】唐诗是中国文学的瑰宝.为了研究计算机上唐诗分类工作中检索关键字的选取，某研究人员将唐诗分成7大类别，并从《全唐诗》48900多篇唐诗中随机抽取了500篇，统计了每个类别及各类别包含“花”、“山”、“帘”字的篇数，得到下表：

    爱情婚姻

    咏史怀古

    边塞战争

    山水田园

    交游送别

    羁旅思乡

    其他

    总计

    篇数

    100

    64

    55

    99

    91

    73

    18

    500

    含“山”字的篇数

    51

    48

    21

    69

    48

    30

    4

    271

    含“帘”字的篇数

    21

    2

    0

    0

    7

    3

    5

    38

    含“花”字的篇数

    60

    6

    14

    17

    32

    28

    3

    160

    （1）根据上表判断，若从《全唐诗》含“山”字的唐诗中随机抽取一篇，则它属于哪个类别的可能性最大，属于哪个类别的可能性最小，并分别估计该唐诗属于这两个类别的概率；

    （2）已知检索关键字的选取规则为：

    ①若有超过95%的把握判断“某字”与“某类别”有关系，则“某字”为“某类别”的关键字；

    ②若“某字”被选为“某类别”关键字，则由其对应列联表得到的的观测值越大，排名就越靠前；

    设“山”“帘”“花”和“爱情婚姻”对应的观测值分别为，，.已知，，请完成下面列联表，并从上述三个字中选出“爱情婚姻”类别的关键字并排名.

    属于“爱情婚姻”类

    不属于“爱情婚姻”类

    总计

    含“花”字的篇数

    不含“花”的篇数

    总计

    附：，其中.

    0.05

    0.025

    0.010

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“微信运动”是手机推出的多款健康运动软件中的一款，某学校140名老师均在微信好友群中参与了“微信运动”，对运动10000步或以上的老师授予“运动达人”称号，低于10000步称为“参与者”，为了解老师们运动情况，选取了老师们在4月28日的运动数据进行分析，统计结果如下：

    运动达人

    参与者

    合计

    男教师

    60

    20

    80

    女教师

    40

    20

    60

    合计

    100

    40

    140

    （Ⅰ）根据上表说明，能否在犯错误概率不超过0.05的前提下认为获得“运动达人”称号与性别有关？

    （Ⅱ）从具有“运动达人”称号的教师中，采用按性别分层抽样的方法选取10人参加全国第四届“万步有约”全国健走激励大赛某赛区的活动，若从选取的10人中随机抽取3人作为代表参加开幕式，设抽取的3人中女教师人数为，写出的分布列并求出数学期望.

    参考公式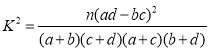：，其中.

    参考数据：

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线上点处的切线方程为．

    （Ⅰ）求抛物线的方程；

    （Ⅱ）设和为抛物线上的两个动点，其中且，线段的垂直平分线与轴交于点，求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的一个顶点和两个焦点构成的三角形的面积为4．

    （1）求椭圆的方程；

    （2）已知直线与椭圆交于、两点，试问，是否存在轴上的点，使得对任意的，为定值，若存在，求出点的坐标，若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某手机企业为确定下一年度投入某种产品的研发费用，统计了近年投入的年研发费用千万元与年销售量千万件的数据，得到散点图1，对数据作出如下处理：令，，得到相关统计量的值如图2：

    （1）利用散点图判断和哪一个更适合作为年研发费用和年销售量的回归类型（不必说明理由），并根据数据，求出与的回归方程；

    （2）已知企业年利润千万元与的关系式为（其中为自然对数的底数），根据（1）的结果，要使得该企业下一年的年利润最大，预计下一年应投入多少研发费用？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种设备随着使用年限的增加，每年的维护费相应增加现对一批该设备进行调查，得到这批设备自购入使用之日起，前5年平均每台设备每年的维护费用大致如下表：

    年份（年）

    1

    2

    3

    4

    5

    维护费（万元）

    1.1

    1.6

    2

    2.5

    2.8

    （1）在这5年中随机抽取两年，求平均每台设备每年的维护费用至少有1年多于2万元的概率；

    （2）求关于的线性回归方程．若该设备的价格是每台16万元，你认为应该使用满五年换一次设备，还是应该使用满八年换一次设备？请说明理由．

    参考公式：用最小二乘法求线性回归方程的系数公式．

    查看答案和解析>>

    同步练习册答案