
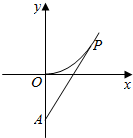
 中国海警缉私船对一艘走私船进行定位:以走私船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度).中国海警缉私船恰在走私船正南方18海里A处(如图).现假设:①走私船的移动路径可视为抛物线y=$\frac{9}{28}$x2;②定位后中国海警缉私船即刻沿直线匀速前往追埔;③中国海警缉私船出发t小时后,走私船所在的位置的横坐标为2$\sqrt{7}$t.
中国海警缉私船对一艘走私船进行定位:以走私船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度).中国海警缉私船恰在走私船正南方18海里A处(如图).现假设:①走私船的移动路径可视为抛物线y=$\frac{9}{28}$x2;②定位后中国海警缉私船即刻沿直线匀速前往追埔;③中国海警缉私船出发t小时后,走私船所在的位置的横坐标为2$\sqrt{7}$t.分析 (1)t=1时,确定P的横坐标,代入抛物线方程可得P的纵坐标,利用|AP|,即可确定中国海警缉私船速度的大小;
(2)设中国海警缉私船的时速为v海里,经过t小时追上走私船,此时位置为(2$\sqrt{7}$t,9t2),从而可得v关于t的关系式,利用基本不等式,即可得到结论.
解答 解:(1)t=1时,P的横坐标xP=2$\sqrt{7}$,代入抛物线方程y=$\frac{9}{28}$x2中,得P的纵坐标yP=9.
由A(0,-18),可得|AP|=$\sqrt{757}$,得中国海警缉私船速度的大小为$\sqrt{757}$海里/时;
(2)设中国海警缉私船的时速为v海里,经过t小时追上走私船,此时位置为(2$\sqrt{7}$t,9t2).
由vt=|AP|=$\sqrt{81({t}^{4}+4)+352{t}^{2}}$,整理得v2=81(t2+$\frac{4}{{t}^{2}}$)+352
因为t2+$\frac{4}{{t}^{2}}$≥4,当且仅当t=$\sqrt{2}$时等号成立,所以v2≥81×4+352=262,即v≥26.
因此,中国海警缉私船的时速至少是26海里才能追上走私船.
点评 本题主要考查函数模型的选择与运用.选择恰当的函数模型是解决此类问题的关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{4\sqrt{5}}}{15}$ | B. | $\frac{{\sqrt{5}}}{15}$ | C. | $\frac{{\sqrt{3}}}{15}$ | D. | $\frac{4}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{15}$ | B. | $\frac{16}{15}$ | C. | $\frac{20}{31}$ | D. | $\frac{40}{31}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②⑤ | B. | ①③⑤ | C. | ②③④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com