
分析 令h(x)=f(x)-g(x),问题转化为满足h(x)在[0,2]上是增函数即可,结合二次函数的性质通过讨论对称轴的位置,解出即可.
解答 解:当x1<x2时都有f(x1)-f(x2)<g(x1)-g(x2),
即x1<x2时都有f(x1)-g(x1)<f(x2)-g(x2),
令h(x)=f(x)-g(x)=x2+bx-|x-1|,
故需满足h(x)在[0,2]上是增函数即可,
①当0≤x<1时,h(x)=x2+(b+1)x-1,
对称轴x=-$\frac{b+1}{2}$≤0,解得:b≥-1,
②当1≤x≤2时,h(x)=x2+(b-1)x+1,
对称轴x=-$\frac{b-1}{2}$≤1,解得:b≥-1,
综上:b≥-1,
故答案为:-1.
点评 本题考察了二次函数的性质、考察转化思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
 将偶数按如图所示的规律排列下去,且用amn表示位于从上到下第m行,从左到右n列的数,比如a22=6,a43=18,若amn=2016,则有 ( )
将偶数按如图所示的规律排列下去,且用amn表示位于从上到下第m行,从左到右n列的数,比如a22=6,a43=18,若amn=2016,则有 ( )| A. | m=44,n=28 | B. | m=44,n=29 | C. | m=45,n=28 | D. | m=45,n=29 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{0,\frac{3}{2}})$ | B. | $({-∞,-\frac{1}{2}})∪[{0,\frac{3}{2}})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $({-∞,-\frac{1}{2}})∪({0,\frac{3}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
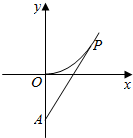 中国海警缉私船对一艘走私船进行定位:以走私船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度).中国海警缉私船恰在走私船正南方18海里A处(如图).现假设:①走私船的移动路径可视为抛物线y=$\frac{9}{28}$x2;②定位后中国海警缉私船即刻沿直线匀速前往追埔;③中国海警缉私船出发t小时后,走私船所在的位置的横坐标为2$\sqrt{7}$t.
中国海警缉私船对一艘走私船进行定位:以走私船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度).中国海警缉私船恰在走私船正南方18海里A处(如图).现假设:①走私船的移动路径可视为抛物线y=$\frac{9}{28}$x2;②定位后中国海警缉私船即刻沿直线匀速前往追埔;③中国海警缉私船出发t小时后,走私船所在的位置的横坐标为2$\sqrt{7}$t.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com