
| A. | $\frac{{4\sqrt{5}}}{15}$ | B. | $\frac{{\sqrt{5}}}{15}$ | C. | $\frac{{\sqrt{3}}}{15}$ | D. | $\frac{4}{15}$ |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线CM与DN所成的角的余弦值.
解答  解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1的棱长为2,
则N(1,2,2),D(0,0,0),C(0,2,0),M(2,2,1),
则$\overrightarrow{CM}$=(2,0,1),$\overrightarrow{DN}$=(1,2,2),
设异面直线所成角为θ,
则cosθ=$\frac{|\overrightarrow{CM}•\overrightarrow{DN}|}{|\overrightarrow{CM}|•|\overrightarrow{DN}|}$=$\frac{4}{\sqrt{5}•\sqrt{9}}$=$\frac{4\sqrt{5}}{15}$.
∴异面直线CM与DN所成的角的余弦值为$\frac{4\sqrt{5}}{15}$.
故选:A.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{0,\frac{3}{2}})$ | B. | $({-∞,-\frac{1}{2}})∪[{0,\frac{3}{2}})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $({-∞,-\frac{1}{2}})∪({0,\frac{3}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 12月10日 | 12月11日 | 12月12日 | 12月13日 | 12月14日 | 12月15日 |
| PM2.5浓度 超过200的部分为x (微克/立方米) | 10 | 11 | 13 | 12 | 8 | 5 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
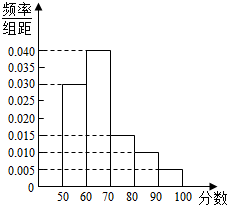 某次考试后,抽取了40位学生的成绩,并根据抽样数据制作的频率分布直方图如图所示,从成绩为[80,100]的学生中随机抽取了2人进行某项调查,则这两人分别来自两个不同分数段内的频率为$\frac{8}{15}$.
某次考试后,抽取了40位学生的成绩,并根据抽样数据制作的频率分布直方图如图所示,从成绩为[80,100]的学生中随机抽取了2人进行某项调查,则这两人分别来自两个不同分数段内的频率为$\frac{8}{15}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
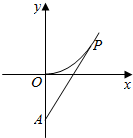 中国海警缉私船对一艘走私船进行定位:以走私船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度).中国海警缉私船恰在走私船正南方18海里A处(如图).现假设:①走私船的移动路径可视为抛物线y=$\frac{9}{28}$x2;②定位后中国海警缉私船即刻沿直线匀速前往追埔;③中国海警缉私船出发t小时后,走私船所在的位置的横坐标为2$\sqrt{7}$t.
中国海警缉私船对一艘走私船进行定位:以走私船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度).中国海警缉私船恰在走私船正南方18海里A处(如图).现假设:①走私船的移动路径可视为抛物线y=$\frac{9}{28}$x2;②定位后中国海警缉私船即刻沿直线匀速前往追埔;③中国海警缉私船出发t小时后,走私船所在的位置的横坐标为2$\sqrt{7}$t.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ 或$\frac{{2\sqrt{2}}}{3}$ | B. | $\sqrt{3}$或$\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$或10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com