
| A. | ①②⑤ | B. | ①③⑤ | C. | ②③④ | D. | ②④ |
分析 ①先求定义域,根据定义域化简函数解析式;
②根据函数奇偶性的定义进行判断.
③根据函数单调性的定义判断.
④根据奇函数的积分性质进行判断.
⑤根据两点间的距离的意义进行判断.
解答 解:要使函数有意义,需满足$\left\{\begin{array}{l}{{x}^{2}-{x}^{4}≥0}\\{|x-2|≠2}\end{array}\right.$,
解得-1≤x≤1且x≠0,即函数的定义域为[-1,0)∪(0,1],故①不正确.
根据函数的定义域可将函数解析式化简为$f(x)=\frac{\sqrt{{x}^{2}-{x}^{4}}}{2-x-2}=-\frac{\sqrt{{x}^{2}-{x}^{4}}}{x}$,
所以$f(-x)=\frac{\sqrt{{x}^{2}-{x}^{4}}}{x}$=-f(x),即函数是奇函数,所以其图象关于原点对称;故②正确,
③∵函数的定义域是间断的,
∴函数在定义域内不单调,故③错误,
④∵函数f(x)在定义域上为奇函数,
∴$\int_a^b{f(x)dx=0}$,故④正确,
⑤∵M,N为函数f(x)图象上任意不同两点,所以|MN|>0,而不是|MN|>$\sqrt{2}$,故⑤错误,
故选:D
点评 本题主要考查与函数有关的命题的真假判断,求出定义域后化简解析式是解决本题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 12月10日 | 12月11日 | 12月12日 | 12月13日 | 12月14日 | 12月15日 |
| PM2.5浓度 超过200的部分为x (微克/立方米) | 10 | 11 | 13 | 12 | 8 | 5 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
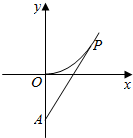 中国海警缉私船对一艘走私船进行定位:以走私船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度).中国海警缉私船恰在走私船正南方18海里A处(如图).现假设:①走私船的移动路径可视为抛物线y=$\frac{9}{28}$x2;②定位后中国海警缉私船即刻沿直线匀速前往追埔;③中国海警缉私船出发t小时后,走私船所在的位置的横坐标为2$\sqrt{7}$t.
中国海警缉私船对一艘走私船进行定位:以走私船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度).中国海警缉私船恰在走私船正南方18海里A处(如图).现假设:①走私船的移动路径可视为抛物线y=$\frac{9}{28}$x2;②定位后中国海警缉私船即刻沿直线匀速前往追埔;③中国海警缉私船出发t小时后,走私船所在的位置的横坐标为2$\sqrt{7}$t.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ 或$\frac{{2\sqrt{2}}}{3}$ | B. | $\sqrt{3}$或$\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$或10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
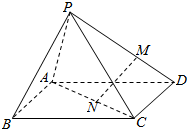 如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB.
如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com