
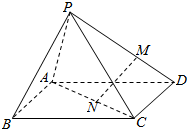
 如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB.
如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB. 分析 建立空间坐标系,设A,C,P三点坐标,用此三点的坐标表示出$\overrightarrow{MN}$,$\overrightarrow{BP}$,$\overrightarrow{BA}$,然后观察能否用$\overrightarrow{BP},\overrightarrow{BA}$表示出$\overrightarrow{MN}$即可判断线面是否平行.
解答 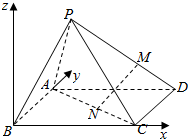 解:建立如图所示的空间坐标系,设C(a,0,0),A(0,b,0),P(m,n,p),则D(a,b,0),
解:建立如图所示的空间坐标系,设C(a,0,0),A(0,b,0),P(m,n,p),则D(a,b,0),
∴$\overrightarrow{BP}$=(m,n,p),$\overrightarrow{BA}$=(0,b,0),$\overrightarrow{CA}$=(-a,b,0),$\overrightarrow{DP}$=(m-a,n-b,p),$\overrightarrow{DC}$=(0,-b,0),
∵$\frac{DM}{MP}$=$\frac{CN}{NA}$,∴$\frac{DM}{DP}=\frac{CN}{CA}$,设$\frac{DM}{DP}=\frac{CN}{CA}$=λ,则$\overrightarrow{DM}$=λ$\overrightarrow{DP}$=(mλ-aλ,nλ-bλ,pλ),$\overrightarrow{CN}$=λ$\overrightarrow{CA}$=(-aλ,bλ,0).
∴$\overrightarrow{MN}$=-$\overrightarrow{DM}$+$\overrightarrow{DC}$+$\overrightarrow{CN}$=(-mλ,2bλ-nλ-b,-pλ),∴$\overrightarrow{MN}$=-λ$\overrightarrow{BP}$+(2λ-1)$\overrightarrow{BA}$.
∵BP?平面PAB,BA?平面PAB,MN?平面PAB,∴MN∥平面PAB.
点评 本题考查了空间向量在立体几何中的应用,属于中档题.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | ①②⑤ | B. | ①③⑤ | C. | ②③④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$或0 | B. | -2或2 | C. | $\sqrt{2}$或-$\sqrt{2}$ | D. | -$\sqrt{2}$或0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某工厂的一个车间包装一种产品,在一定的时间内,从自动包装传送带上,每隔30min抽一包产品,称其重量是否合格,记录抽查产品的重量的茎叶图如图所示(以重量的个位数为叶),则抽查产品重量的中位数和众数分别为( )
某工厂的一个车间包装一种产品,在一定的时间内,从自动包装传送带上,每隔30min抽一包产品,称其重量是否合格,记录抽查产品的重量的茎叶图如图所示(以重量的个位数为叶),则抽查产品重量的中位数和众数分别为( )| A. | 96,98 | B. | 96,99 | C. | 98,98 | D. | 98,99 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 3lg2 | D. | 3log23 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com