
分析 设$\overrightarrow{a}$=(m,n),由题意可得n=1,再由向量的模的公式,可得m=-1或-3,再由$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$,计算即可得到所求.
解答 解:设$\overrightarrow{a}$=(m,n),由$\overrightarrow{b}$=(2,-1),
$\overrightarrow{a}$+$\overrightarrow{b}$垂直于y轴,可得n=1,
又|$\overrightarrow{a}$+$\overrightarrow{b}$|=1,可得|m+2|=1,
解得m=-1或-3,
即有$\overrightarrow{a}$=(-1,1)或(-3,1),
则$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$=$\frac{-2-1}{\sqrt{2}}$=-$\frac{3\sqrt{2}}{2}$;
或$\frac{-6-1}{\sqrt{10}}$=-$\frac{7\sqrt{10}}{10}$.
故答案为:-$\frac{3\sqrt{2}}{2}$或-$\frac{7\sqrt{10}}{10}$.
点评 本题考查向量的投影的求法,注意运用向量的数量积和模的公式,考查运算能力,属于中档题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
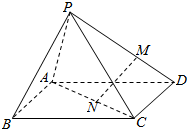 如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB.
如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{|a|}{\sqrt{1+{a}^{2}}}$ | B. | $\frac{a}{\sqrt{1+{a}^{2}}}$ | C. | -$\frac{a}{\sqrt{1+{a}^{2}}}$ | D. | -$\frac{1}{\sqrt{1+{a}^{2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{8}{27}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 72 | B. | 96 | C. | 144 | D. | 288 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com