
分析 把二次函数的解析式f(x)化为顶点形式,找出抛物线的对称轴,然后根据对称轴与区间位置关系,分类讨论,即可求函数f(x)=-x2+2ax-1在[0,2]上的最大值、最小值.
解答 解:由f(x)=-x2+2ax-1=-(x-a)2+a2-1,0≤x≤2,
∴当a≤0时,最大值g(a)=f(0)=-1;最小值h(a)=f(2)=2a-5;
当0<a≤1时,最大值g(a)=f(a)=a2-1;最小值h(a)=f(2)=2a-5;
当1<a<2时,最大值g(a)=f(a)=a2-1;最小值h(a)=f(0)=-1;
当a≥2时,最大值g(a)=f(2)=2a-5;最小值h(a)=f(0)=-1.
点评 本题主要考查了二次函数的最值,利用函数的图象将对称轴移动,合理地进行分类,从而求得函数的最值,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
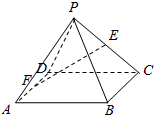 如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.
如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产品数量x | 0 | 3 | 4 | 6 | 7.2 | 10 |
| 生产成本y | 50 | 72.5 | 82 | 104 | 119.2 | 160 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com