
设等比数列{an}的前n项和为Sn,已知an + 1 = 2Sn + 2 (n∈N*).
(1)求数列{an}的通项公式;
(2)在an与an + 1之间插入n个数,使这n + 2个数组成一个公差为dn的等差数列.
①在数列{dn}中是否存在三项dm,dk,dp (其中m,k,p成等差数列)成等比数列?若存在,求出这样的三项,若不存在,说明理由;
②求证: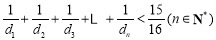 .
.
(1)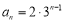 (2)不存在(证明见解析) (3)证明见解析
(2)不存在(证明见解析) (3)证明见解析
【解析】
试题分析:(1)利用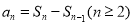 和等比数列的定义即可得出;
和等比数列的定义即可得出;
(2)利用等差数列的通向公式即可得出;
①假设在数列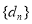 中存在三项
中存在三项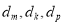 (其中
(其中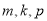 是等差数列)成等比数列,利用等差数列和等比数列的定义及其反证法即可得出;
是等差数列)成等比数列,利用等差数列和等比数列的定义及其反证法即可得出;
②利用(2)的结论、“错位相减法”和等比数列的前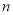 和公式即可得出.
和公式即可得出.
试题解析:(1)【解析】
由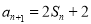 ,得:
,得: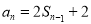
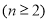
两式相减: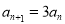
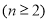
∵数列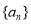 是等比数列,∴
是等比数列,∴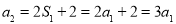 ,故
,故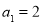
因此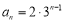 .
.
(2)【解析】
由题意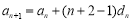 ,即
,即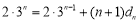 ,故
,故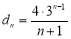
①假设在数列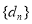 中存在三项
中存在三项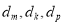 (其中
(其中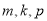 是等差数列)成等比数列
是等差数列)成等比数列
则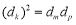 ,即:
,即: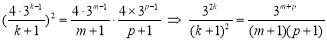 (*)
(*)
∵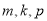 成等差数列,∴
成等差数列,∴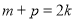
(*)可以化为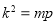 ,故
,故 ,这与题设矛盾
,这与题设矛盾
∴在数列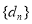 中不存在三项
中不存在三项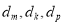 (其中
(其中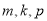 是等差数列)成等比数列.
是等差数列)成等比数列.
②令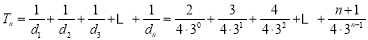
则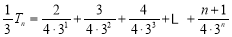
两式相减得: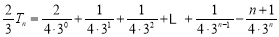
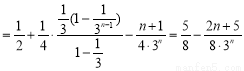
∴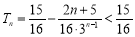 .
.
考点:等差数列和等比数列的性质;错位相减法求和.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源:2016届湖北省高一下学期期中考试文科数学卷(解析版) 题型:填空题
在如下数表中,已知每行、每列中的数都成等差数列,那么,位于下表中的第n行第n+1列的数是 .

查看答案和解析>>
科目:高中数学 来源:2016届湖北省襄阳市调研高一统一测试数学试卷(解析版) 题型:选择题
对于平面α和共面的直线m、n,下列命题正确的是( )
A.若m、n与α所成的角相等,则m∥n
B.若m∥α,n∥α,则m∥n
C.若m⊥α,m⊥n,则n∥α
D.若m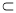 α,n∥α,则m∥n
α,n∥α,则m∥n
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com