练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知的展开式中第5项与第7项的二项数系数相等，且展开式的各项系数之和为1024，则下列说法正确的是（ ）

    A.展开式中奇数项的二项式系数和为256

    B.展开式中第6项的系数最大

    C.展开式中存在常数项

    D.展开式中含项的系数为45

    【答案】BCD

    【解析】

    由二项式的展开式中第5项与第7项的二项数系数相等可知,由展开式的各项系数之和为1024可得,则二项式为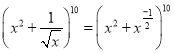,易得该二项式展开式的二项式系数与系数相同,利用二项式系数的对称性判断A,B；根据通项判断C,D即可.

    由二项式的展开式中第5项与第7项的二项数系数相等可知,

    又展开式的各项系数之和为1024,即当时,,所以,

    所以二项式为,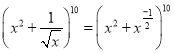

    则二项式系数和为,则奇数项的二项式系数和为,故A错误；

    由可知展开式共有11项,中间项的二项式系数最大,即第6项的二项式系数最大,

    因为与的系数均为1,则该二项式展开式的二项式系数与系数相同,所以第6项的系数最大,故B正确；

    若展开式中存在常数项,由通项可得,解得,故C正确；

    由通项可得,解得,所以系数为,故D正确,

    故选: BCD

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知直线：与抛物线切于点，直线：过定点Q，且抛物线上的点到点Q的距离与其到准线距离之和的最小值为.

    （1）求抛物线的方程及点的坐标；

    （2）设直线与抛物线交于(异于点P)两个不同的点A、B，直线PA，PB的斜率分别为，那么是否存在实数，使得？若存在，求出的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l1：x+2y+1=0，l2：-2x+y+2=0，它们相交于点A.

    (1)判断直线l1和l2是否垂直？请给出理由.

    (2)求过点A且与直线l3：3x+y+4=0平行的直线方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】研究发现，在分钟的一节课中，注力指标与学生听课时间（单位：分钟）之间的函数关系为.

    (1)在上课期间的前分钟内（包括第分钟），求注意力指标的最大值；

    (2)根据专家研究，当注意力指标大于时，学生的学习效果最佳，现有一节分钟课，其核心内容为连续的分钟，问：教师是否能够安排核心内容的时间段，使得学生在核心内容的这段时间内，学习效果均在最佳状态？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若存在集合A、B满足，，则称为的一个二分划.①设，，判断是否为的一个二分划，说明理由.

    ②是否能找到的一个二分划满足集合A中不存在三个成等比数列的数；集合B中不存在无穷的等比数列？说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中为实数.

    （1）试确定函数的奇偶性；

    （2）若函数在区间上单调递增，求的取值范围；

    （3）若函数在区间上有唯一的零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数，，已知函数，的图象存在唯一的公切线.

    （1）求的值；

    （2）当，时，证明：关于的不等式在上有解.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设 是三个不重合的平面，l是直线，给出下列命题

    ①若，则；

    ②若l上两点到的距离相等，则；

    ③若 ，，则；

    ④若， ，且，则．

    其中正确的命题的序号是

    A. ①③ B. ③④ C. ②③ D. ①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一盒中装有12个球，其中5个红球，4个黑球，2个白球，1个绿球；从中随机取出1球，求：

    （1）取出1球是红球的概率；

    （2）取出1球是绿球或黑球或白球的概率.

    查看答案和解析>>

    同步练习册答案