
【题目】已知直线![]() :
:![]() 与抛物线
与抛物线![]() 切于点
切于点![]() ,直线
,直线![]() :
:![]() 过定点Q,且抛物线
过定点Q,且抛物线![]() 上的点到点Q的距离与其到准线距离之和的最小值为
上的点到点Q的距离与其到准线距离之和的最小值为![]() .
.
(1)求抛物线![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(2)设直线![]() 与抛物线
与抛物线![]() 交于(异于点P)两个不同的点A、B,直线PA,PB的斜率分别为
交于(异于点P)两个不同的点A、B,直线PA,PB的斜率分别为![]() ,那么是否存在实数
,那么是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ,(1,2);(2)存在,
,(1,2);(2)存在,![]()
【解析】
(1)由直线![]() 恒过点点及抛物线C上的点到点Q的距离与到准线的距离之和的最小值为
恒过点点及抛物线C上的点到点Q的距离与到准线的距离之和的最小值为![]() ,求出抛物线的方程,再由直线
,求出抛物线的方程,再由直线![]() 与抛物线相切,即可求得切点的坐标;
与抛物线相切,即可求得切点的坐标;
(2)直线![]() 与抛物线方程联立,利用根与系数的关系,求得直线PA,PB的斜率,求出斜率之和为定值,即存在实数
与抛物线方程联立,利用根与系数的关系,求得直线PA,PB的斜率,求出斜率之和为定值,即存在实数![]() 使得斜率之和为定值.
使得斜率之和为定值.
(1)由题意,直线![]() 变为2x+1-m(2y+1)=0,所以定点Q的坐标为
变为2x+1-m(2y+1)=0,所以定点Q的坐标为![]()
抛物线![]() 的焦点坐标
的焦点坐标![]() ,
,
由抛物线C上的点到点Q的距离与到其焦点F的距离之和的最小值为![]() ,
,
可得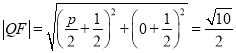 ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
故抛物线C的方程为![]()
又由![]() 消去y得
消去y得![]() ,
,
因为直线![]() 与抛物线C相切,所以
与抛物线C相切,所以![]() ,解得
,解得![]() ,
,
此时![]() ,所以点P坐标为(1,2)
,所以点P坐标为(1,2)
(2)设存在满足条件的实数![]() ,点
,点![]() ,
,
联立![]() ,消去x得
,消去x得![]() ,
,
则![]() ,
,
依题意,可得![]() ,解得m<-1或
,解得m<-1或![]() ,
,
由(1)知P(1,2),
可得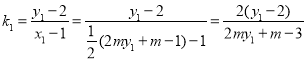 ,
,
同理可得![]() ,
,
所以![]()
=![]() ,
,
故存在实数![]() =
=![]() 满足条件.
满足条件.


科目:高中数学 来源: 题型:
【题目】光伏发电是利用太阳能电池及相关设备将太阳光能直接转化为电能,近几年在国内出台的光伏发电补贴政策的引导下,某地光伏发电装机量急剧上涨,如下表:
年份 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
新增光伏装机量 | 0.4 | 0.8 | 1.6 | 3.1 | 6.1 | 7.1 | 9.7 | 12.2 |
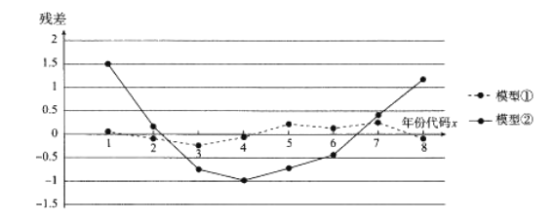
某位同学分别用两种模型:①![]() ,②
,②![]() 进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于
进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于![]() )
)
经过计算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由.
(2)根据(1)的判断结果及表中数据建立![]() 关于
关于![]() 的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
附:归直线的斜率和截距的最小二乘估计公式分别为: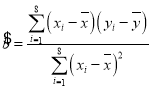 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某一电视台对年龄高于40岁和不高于40岁的人是否喜欢西班牙队进行调查,40岁以上调查了50人,不高于40岁调查了50人,所得数据制成如下列联表:
不喜欢西班牙队 | 喜欢西班牙队 | 总计 | |
40岁以上 |
|
| 50 |
不高于40岁 | 15 | 35 | 50 |
总计 |
|
| 100 |
已知工作人员从所有统计结果中任取一个,取到喜欢西班牙队的人的概率为![]() ,则有超过________的把握认为年龄与西班牙队的被喜欢程度有关.
,则有超过________的把握认为年龄与西班牙队的被喜欢程度有关.
参考公式与临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①经过定点![]() 的直线都可以用方程
的直线都可以用方程![]() 表示;
表示;
②经过定点![]() 的直线都可以用方程
的直线都可以用方程![]() 表示;
表示;
③不经过原点的直线都可以用方程![]() 表示;
表示;
④经过任意两个不同的点![]() 、
、![]() 的直线都可以用方程
的直线都可以用方程![]() 表示,
表示,
其中真命题的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为美化城市环境,相关部门需对一半圆形中心广场进行改造出新,为保障市民安全,施工队对广场进行围挡施工.如图,围挡经过直径的两端点A,B及圆周上两点C,D围成一个多边形ABPQR,其中AR,RQ,QP,PB分别与半圆相切于点A,D,C,B.已知该半圆半径OA长30米,∠COD为60°,设∠BOC为![]() .
.
(1)求围挡内部四边形OCQD的面积;
(2)为减少对市民出行的影响,围挡部分面积要尽可能小.求该围挡内部多边形ABPQR面积的最小值?并写出此时![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1;
(2)若函数f(x)在R上单调递增,求实数a的取值范围;
(3)是否存在实数a,使不等式f(x)≥2x-3对任意x∈R恒成立?若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前7次考试的数学成绩![]() 、物理成绩
、物理成绩![]() 进行分析.下面是该生7次考试的成绩.
进行分析.下面是该生7次考试的成绩.
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)他的数学成绩与物理成绩哪个更稳定?请给出你的证明;
(2)已知该生的物理成绩![]() 与数学成绩
与数学成绩![]() 是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理建议.
是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理建议.
参考公式:方差公式:![]() ,其中
,其中![]() 为样本平均数.
为样本平均数. ,
,![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的展开式中第5项与第7项的二项数系数相等,且展开式的各项系数之和为1024,则下列说法正确的是( )
的展开式中第5项与第7项的二项数系数相等,且展开式的各项系数之和为1024,则下列说法正确的是( )
A.展开式中奇数项的二项式系数和为256
B.展开式中第6项的系数最大
C.展开式中存在常数项
D.展开式中含![]() 项的系数为45
项的系数为45
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com