
(本小题满分12分)某大型企业一天中不同时刻的用电量 (单位:万千瓦时)关于时间
(单位:万千瓦时)关于时间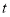 (
(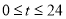 ,单位:小时)的函数
,单位:小时)的函数 近似地满足
近似地满足 ,下图是该企业一天中在0点至12点时间段用电量
,下图是该企业一天中在0点至12点时间段用电量 与时间
与时间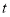 的大致图象.
的大致图象.
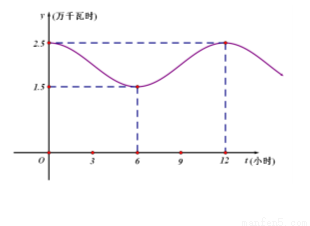
(Ⅰ)根据图象,求 ,
, ,
, ,
, 的值;
的值;
(Ⅱ)若某日的供电量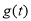 (万千瓦时)与时间
(万千瓦时)与时间 (小时)近似满足函数关系式
(小时)近似满足函数关系式 (
(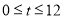 ).当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法计算该企业当日停产的大致时刻(精确度0.1).
).当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法计算该企业当日停产的大致时刻(精确度0.1).
参考数据:
| 10 | 11 | 12 | 11.5 | 11.25 | 11.75 | 11.625 | 11.6875 |
| 2.25 | 2.433 | 2.5 | 2.48 | 2.462 | 2.496 | 2.490 | 2.493 |
| 5 | 3.5 | 2 | 2.75 | 3. 125 | 2.375 | 2.563 | 2.469 |
(Ⅰ) ,
, ,
, ,
, ;(Ⅱ)11.625时(允许取近似值)
;(Ⅱ)11.625时(允许取近似值)
【解析】
试题分析:(Ⅰ)利用图形语言,可以逐一求得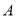 ,
,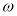 ,
,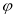 ,
,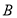 的值;(Ⅱ)即是求f(t)与g(t)的交点横坐标,利用二分法求零点的策略,可以逐步缩小交点横坐标的范围,达到0.1的精确度即可.
的值;(Ⅱ)即是求f(t)与g(t)的交点横坐标,利用二分法求零点的策略,可以逐步缩小交点横坐标的范围,达到0.1的精确度即可.
试题解析:(Ⅰ)由图知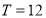 ,
, . 1分
. 1分
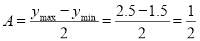 ,
,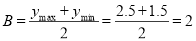 . 2分
. 2分
∴ .
.
又函数 过点
过点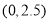 .
.
代入,得 ,又
,又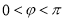 ,∴
,∴ . 2分
. 2分
综上, ,
, ,
, ,
, . 1分
. 1分
即 .
.
(Ⅱ)令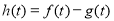 ,设
,设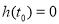 ,则
,则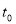 为该企业的停产时间.
为该企业的停产时间.
由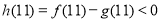 ,
,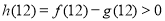 ,则
,则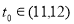 .
.
又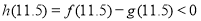 ,则
,则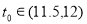 .
.
又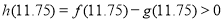 ,则
,则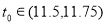 .
.
又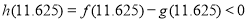 ,则
,则 .
.
又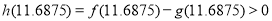 ,则
,则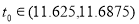 . 4分
. 4分
∵ . 1分
. 1分
∴应该在11.625时停产. 1分
(也可直接由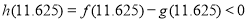 ,
,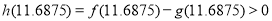 ,得出
,得出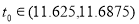 ;答案在11.625—11.6875之间都是正确的;若换算成时间应为11点37分到11点41分停产)
;答案在11.625—11.6875之间都是正确的;若换算成时间应为11点37分到11点41分停产)
考点:三角函数图象与性质,恒等变形,二分法求零点,数学知识和方法的实际应用


科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
已知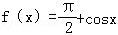 ,则f′(
,则f′(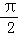 )=( )
)=( )
A.﹣1+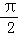 B.﹣1 C.1 D.0
B.﹣1 C.1 D.0
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.1从平面向量到空间向量练习卷(解析版) 题型:选择题
空间中,与向量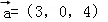 同向共线的单位向量
同向共线的单位向量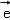 为( )
为( )
A.
B. 或
或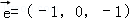
C.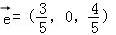
D.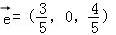 或
或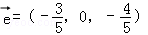
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测文科数学试卷(解析版) 题型:选择题
如图,已知正方体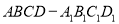 棱长为4,点
棱长为4,点 在棱
在棱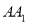 上,且
上,且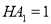 .点
.点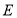 ,
,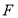 分别为棱
分别为棱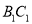 ,
,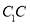 的中点,
的中点,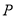 是侧面
是侧面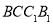 内一动点,且满足
内一动点,且满足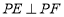 .则当点
.则当点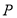 运动时,
运动时,  的最小值是
的最小值是
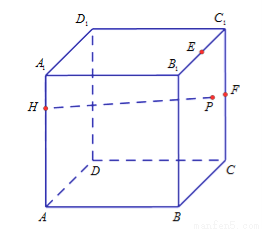
(A)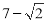 (B)
(B)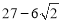
(C) (D)
(D)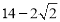
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测文科数学试卷(解析版) 题型:选择题
命题“若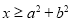 ,则
,则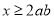 ”的逆命题是
”的逆命题是
(A)若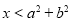 ,则
,则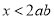
(B)若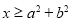 ,则
,则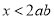
(C)若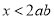 ,则
,则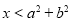
(D)若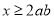 ,则
,则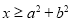
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:填空题
已知定义在R上的奇函数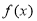 ,当
,当 时,
时,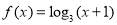 .若关于
.若关于 的不等式
的不等式 的解集为
的解集为 ,函数
,函数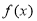 在
在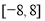 上的值域为
上的值域为 ,若“
,若“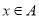 ”是“
”是“ ”的充分不必要条件,则实数
”的充分不必要条件,则实数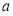 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:选择题
已知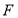 是椭圆
是椭圆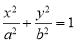 (
(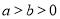 )的左焦点,
)的左焦点,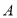 为右顶点,
为右顶点,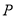 是椭圆上一点,
是椭圆上一点,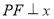 轴.若
轴.若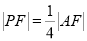 ,则该椭圆的离心率是( )
,则该椭圆的离心率是( )
(A) (B)
(B) (C)
(C) (D)
(D)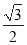
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市黄浦区高三上学期期终调研测试文科数学试卷(解析版) 题型:填空题
已知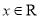 ,定义:
,定义: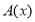 表示不小于
表示不小于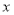 的最小整数.如
的最小整数.如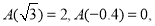
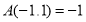 .若
.若 ,则实数
,则实数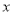 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省莱州市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
已知函数 ,其中e是自然对数的底数,若直线
,其中e是自然对数的底数,若直线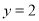 与函数
与函数 的图象有三个交点,则实数
的图象有三个交点,则实数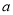 的取值范围是
的取值范围是
A. B.
B.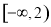 C.
C.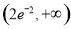 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com