
【题目】已知α∈(0, ![]() ),β∈(0,
),β∈(0, ![]() ),且满足
),且满足 ![]() cos2
cos2 ![]() +
+ ![]() sin2
sin2 ![]() =
= ![]() +
+ ![]() ,sin(2017π﹣α)=
,sin(2017π﹣α)= ![]() cos(
cos( ![]() π﹣β),则α+β= .
π﹣β),则α+β= .
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1中,E,F,H分别为A1B1 , B1C1 , CC1的中点.
(Ⅰ)证明:BE⊥AH;
(Ⅱ)在棱D1C1上是否存在一点G,使得AG∥平面BEF?若存在,求出点G的位置;若不存在,请说明理由.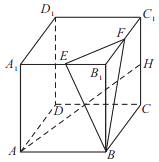
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)当a=b=1时,求满足f(x)=3x的x的值;
(2)若函数f(x)是定义在R上的奇函数,
①判断f(x)在R的单调性并用定义法证明;
②当x≠0时,函数g(x)满足f(x)[g(x)+2]= ![]() (3﹣x﹣3x),若对任意x∈R且x≠0,不等式g(2x)≥mg(x)﹣11恒成立,求实数m的最大值.
(3﹣x﹣3x),若对任意x∈R且x≠0,不等式g(2x)≥mg(x)﹣11恒成立,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.x,y∈R,若x+y≠0,则x≠1且y≠﹣1
B.命题“x∈R,使得x2+2x+3<0”的否定是“x∈R,都有x2+2x+3>0”
C.a∈R,“ ![]() <1”是“a>1”的必要不充分条件
<1”是“a>1”的必要不充分条件
D.“若am2<bm2 , 则a<b”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点, ![]() =(2cosx,
=(2cosx, ![]() ),
), ![]() =(sinx+
=(sinx+ ![]() cosx,﹣1),若f(x)=
cosx,﹣1),若f(x)= ![]()
![]() +2.
+2.
(1)求函数f(x)的对称轴方程;
(2)当 ![]() 时,若函数g(x)=f(x)+m有零点,求m的范围.
时,若函数g(x)=f(x)+m有零点,求m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中, ![]() =
= ![]() +
+ ![]()
(Ⅰ)求△ABM与△ABC的面积之比
(Ⅱ)若N为AB中点, ![]() 与
与 ![]() 交于点P且
交于点P且 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R),求x+y的值.
(x,y∈R),求x+y的值.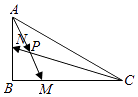
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=-x3-2x2+4x,当x∈[-3,3]时,f(x)≥a有恒成立,则实数a的取值范围是( )
A.(-3,11)
B.[-33,+∞)
C.(-∞,-33]
D.[2,7]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,游乐场中的摩天轮匀速逆时针旋转,每转一圈需要6min,其中心O距离地面40.5m,摩天轮的半径为40m,已知摩天轮上点P的起始位置在最低点处,在时刻t(min)时点P距离地面的高度为f(t)=Asin(ωt+φ)+h(A>0,ω>0,﹣π<φ<0,t≥0).
(Ⅰ)求f(t)的单调减区间;
(Ⅱ)求证:f(t)+f(t+2)+f(t+4)是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相互统一的和谐美.定义:能够将圆O的周长和面积同时等分成两部分的函数称为圆煌一个“太极函数”下列有关说法中: 
①对圆O:x2+y2=1的所有非常数函数的太极函数中,一定不能为偶函数;
②函数f(x)=sinx+1是圆O:x2+(y﹣1)2=1的一个太极函数;
③存在圆O,使得f(x)= ![]() 是圆O的太极函数;
是圆O的太极函数;
④直线(m+1)x﹣(2m+1)y﹣1=0所对应的函数一定是圆O:(x﹣2)2+(y﹣1)2=R2(R>0)的太极函数.
所有正确说法的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com