
甲、乙两人破译一密码,它们能破译的概率分别为 和
和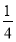 ,试求:
,试求:
(1)两人都能破译的概率;
(2)两人都不能破译的概率;
(3)恰有一人能破译的概率;
(4)至多有一人能破译的概率;
(5)若要使破译的概率为99%,至少需要多少乙这样的人?
(1) (2)
(2)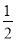 (3)
(3)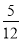 (4)
(4)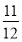 (5)16个
(5)16个
【解析】
解:设事件A为“甲能译出”,事件B为“乙能译出”,则A、B相互独立,从而A与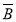 、
、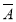 与B、
与B、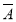 与
与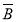 均相互独立.
均相互独立.
(1)“两人都能译出”为事件AB,则
P(AB)=P(A)P(B)=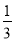 ×
×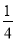 =
= .
.
(2)“两人都不能译出”为事件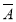
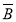 ,则
,则
P(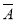
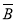 )=P(
)=P(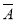 )P(
)P(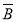 )=[1-P(A)][1-P(B)]
)=[1-P(A)][1-P(B)]
=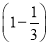
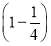 =
=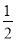 .
.
(3)“恰有一人能译出”为事件A +
+ B,又A
B,又A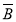 与
与 B互斥,则P(A
B互斥,则P(A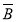 +
+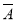 B)=P(A
B)=P(A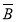 )+P(
)+P(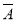 B)
B)
=P(A)P( )+P(
)+P(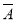 )P(B)
)P(B)
=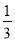 ×
×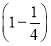 +
+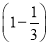 ×
×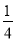 =
=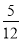 .
.
(4)“至多一人能译出”为事件A +
+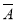 B+
B+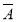
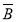 ,且A
,且A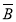 、
、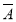 B、
B、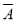
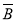 互斥,故
互斥,故
P(A +
+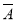 B+
B+
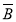 )
)
=P(A)P(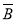 )+P(
)+P(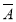 )P(B)+P(
)P(B)+P( )P(
)P(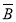 )
)
=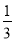 ×
×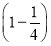 +
+ ×
×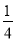 +
+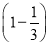 ×
×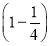 =
=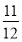 .
.
(5)设至少需n个乙这样的人,而n个乙这样的人译不出的概率为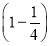 n,故n个乙这样的人能译出的概率为1-
n,故n个乙这样的人能译出的概率为1- n≈99%.
n≈99%.
解得n=16.
故至少需16个乙这样的人,才能使译出的概率为99%.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.5练习卷(解析版) 题型:填空题
设一随机试验的结果只有A和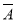 ,且P(A)=p令随机变量X=
,且P(A)=p令随机变量X= ,则X的方差V(X)等于________.
,则X的方差V(X)等于________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.4练习卷(解析版) 题型:选择题
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类.这三类工程所含项目的个数分别占总数的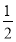 、
、 、
、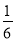 ,现在3名工人独立地从中任选一个项目参与建设.
,现在3名工人独立地从中任选一个项目参与建设.
(1)求他们选择的项目所属类别互不相同的概率;
(2)记X为3人中选择的项目属于基础设施工程或产业建设工程的人数,求X的分布列.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.4练习卷(解析版) 题型:填空题
已知一个射手每次击中目标的概率为p=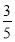 ,他在4次射击中,命中两次的概率为________,刚好在第二、第三两次击中目标的概率为________.
,他在4次射击中,命中两次的概率为________,刚好在第二、第三两次击中目标的概率为________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.3练习卷(解析版) 题型:填空题
甲、乙、丙三人将参加某项测试,他们能达标的概率分别是0.8,0.6,0.5,则三人都达标的概率为________,三人中至少有一人达标的概率为________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.3练习卷(解析版) 题型:解答题
1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,问从2号箱取出红球的概率是多少?
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.2练习卷(解析版) 题型:填空题
一个盒子里装有相同大小的黑球10个,红球12个,白球4个.从中任取两个,其中白球的个数记为X,则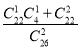 等于________(用概率的式子表示).
等于________(用概率的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com