【题目】
本相同的资料书配给三个班级，要求每班至少一本且至多六本，则不同的分配方法共有_____种．
【答案】25.
【解析】
先由题，将
本相同的资料书配给三个班级，要求每班至少一本且至多六本，进行分组，再分别计算每一组的情况，最后求得答案.
先分组，再排序，12本书分三个班级，且每班至少一本且至多六本，可能有
1、5、6；2、4、6；2、5、5；3、3、6；3、4、5；4、4、4共6中情况
当一个班分1本，一个班分5本，一个班分6本，不同的方法有
种；
当一个班分2本，一个班分4本，一个班分6本，不同的方法有种；
当一个班分2本，一个班分5本，一个班分5本，不同的方法有
种；
当一个班分3本，一个班分3本，一个班分6本，不同的方法有种；
当一个班分3本，一个班分4本，一个班分5本，不同的方法有种；
当一个班分4本，一个班分4本，一个班分4本，不同的方法有
种；
所以一共有
故答案为25
计算高手系列答案科目：高中数学 来源： 题型：
【题目】某纺织厂为了生产一种高端布料，准备从
农场购进一批优质棉花，厂方技术人员从农场存储的优质棉花中随机抽取了
处棉花，分别测量了其纤维长度（单位：
）的均值，收集到个样本数据，并制成如下频数分布表：
（1）求这个样本数据的平均数和样本方差（同一组数据用该区间的中点值作代表）；
（2）将收集到的数据绘制成直方图可以认为这批棉花的纤维长度服从分布
，其中
.
①利用正态分布，求
；
②纺织厂将农场送来的这批优质棉进行二次检验，从中随机抽取
处测量其纤维均值
，数据如下：
若个样本中纤维均值
的频率不低于①中，即可判断该批优质棉花合格，否则认为农场运送是掺杂了次品，判断该批棉花不合格.按照此依据判断农场送来的这批棉花是否为合格的优质棉花，并说明理由.
附：若
，则
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
、
两个班共有65名学生，为调查他们的引体向上锻炼情况，通过分层抽样获得了部分学生引体向上的测试数据（单位：个），用茎叶图记录如下：
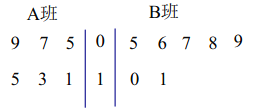
(1)试估计班的学生人数；
(2)从班和班抽出的学生中，各随机选取一人，班选出的人记为甲，班选出的人记为乙，假设所有学生的测试相对独立，比较甲、乙两人的测试数据得到随机变量
.规定：当甲的测试数据比乙的测试数据低时，记
；当甲的测试数据与乙的测试数据相等时，记
；当甲的测试数据比乙的测试数据高时，记
.求随机变量的分布列及数学期望.
(3)再从、两个班中各随机抽取一名学生，他们引体向上的测试数据分别是10，8（单位：个），这2个新数据与表格中的数据构成的新样本的平均数记
，表格中数据的平均数记为
，试判断和的大小.（结论不要求证明）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在长方体
中，
，点E是棱
上的一个动点，若平面
交棱
于点
，给出下列命题：
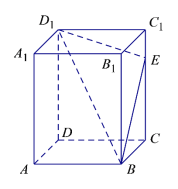
①四棱锥
的体积恒为定值；
②存在点
，使得
平面
；
③对于棱上任意一点，在棱
上均有相应的点
，使得
平面
；
④存在唯一的点，使得截面四边形
的周长取得最小值.
其中真命题的是____________．（填写所有正确答案的序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆心在x轴上的圆C与直线
切于点
，圆
.
（1）求圆C的标准方程；
（2）已知
，圆P与x轴相交于两点
（点M在点N的右侧），过点M任作一条倾斜角不为0的直线与圆C相交于
两点.问：是否存在实数a，使得
？若存在，求出实数a的值，若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱柱ABCD﹣A1B1C1D1中，底面四边形ABCD是矩形，平面DCC1D1⊥平面ABCD.AD=3，CD=DD1=5，∠D1DC=120°，M，N分别是线段AD1，BD的中点.
（1）求证：MN//平面DCC1D1；
（2）求证：MN⊥平面ADC1；
（3）求三棱锥D1﹣ADC1的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】重庆某地区
年至
年农村居民家庭人均纯收入
（单位：万元）的数据如表：
年份 |
|
|
|
|
|
年份代号 |
|
|
|
|
|
纯收入 |
|
|
|
|
|
（1）求关于
的线性回归方程；
（2）利用（1）中的回归方程，分析年至年该地区农村居民家庭人均纯收入的变化情况，并预测该地区
年农村居民家庭人均纯收入.
附：回归直线的斜率和截距的最小二乘法估计公式分别为：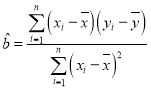
，
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
