
分析 由x>$\frac{3}{2}$,可得2x-3>0,即有函数y=2x+$\frac{4}{2x-3}$=(2x-3)+$\frac{4}{2x-3}$+3,运用基本不等式可得最小值,并求得等号成立的条件.
解答 解:由x>$\frac{3}{2}$,可得2x-3>0,
则函数y=2x+$\frac{4}{2x-3}$
=(2x-3)+$\frac{4}{2x-3}$+3
≥2$\sqrt{(2x-3)•\frac{4}{2x-3}}$+3=7.
当且仅当2x-3=2,即x=$\frac{5}{2}$时,取得最小值7.
故答案为:7.
点评 本题考查基本不等式的运用:求最值,注意运用变形的技巧和满足的条件:一正二定三等,考查运算能力,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
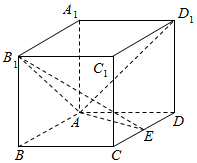 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,E为CD上任意一点.
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,E为CD上任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{2},1)$ | B. | (0,1) | C. | $(0,\frac{1}{2}]$ | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱 | 不喜爱 | 总计 | |
| 男学生 | 60 | 80 | |
| 女学生 | |||
| 总计 | 70 | 30 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
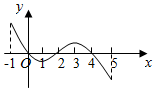 已知函数f(x)的定义域为[-1,5],部分对应值如表,y=f'(x)的图象如图所示,下列关于函数f(x)的命题:
已知函数f(x)的定义域为[-1,5],部分对应值如表,y=f'(x)的图象如图所示,下列关于函数f(x)的命题:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com