
分析 根据已知条件an+1+3an=0得到$\frac{{a}_{n+1}}{{a}_{n}}$=-3,可知数列{an}是首项为a1=-1、公比为-3的等比数列,结合等比数列的通项公式和前n项和公式进行解答即可.
解答 解:∵an+1+3an=0,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=-3,
又∵a1=-1,
∴数列{an}是首项为a1=-1、公比q=-3的等比数列,
∴an=a1•qn-1=-1×(-3)n-1=-(-3)n-1.
Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$=$\frac{-1×[1-(-3)^{n}]}{1-(-3)}$=-$\frac{1-(-3)^{n}}{4}$.
点评 本题考查了等比数列的基本知识,考查了学生的计算能力,解题时要认真审题,仔细解答,避免错误,属于基础题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}{a^2}$ | B. | $-\frac{{\sqrt{3}}}{2}{a^2}$ | C. | $\frac{1}{2}{a^2}$ | D. | $\frac{{\sqrt{3}}}{2}{a^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在四边形ABCD中,AB⊥BC,AB=3,BC=4,△ACD是等边三角形,则$\overrightarrow{AC}•\overrightarrow{BD}$的值为$\frac{7}{2}$.
如图,在四边形ABCD中,AB⊥BC,AB=3,BC=4,△ACD是等边三角形,则$\overrightarrow{AC}•\overrightarrow{BD}$的值为$\frac{7}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
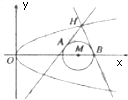 如图,已知⊙M:(x-4)2+y2=1和抛物线C:y2=2px(p>0,其焦点为F),且$\overrightarrow{FM}$=($\frac{15}{4}$,0,),过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切于A、B两点.
如图,已知⊙M:(x-4)2+y2=1和抛物线C:y2=2px(p>0,其焦点为F),且$\overrightarrow{FM}$=($\frac{15}{4}$,0,),过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,四边形ABCD的顶点都在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,对角线AC与BD分别过椭圆的左焦点F1(-1,0)和右焦点F2(1,0),且AC⊥BD,椭圆的一条准线方程为x=4.
如图,在平面直角坐标系xOy中,四边形ABCD的顶点都在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,对角线AC与BD分别过椭圆的左焦点F1(-1,0)和右焦点F2(1,0),且AC⊥BD,椭圆的一条准线方程为x=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若{dn}满足dn=$\frac{{{b_1}+2{b_2}+3{b_3}+…+n{b_n}}}{1+2+3+…n}$,则{dn}也是等比数列 | |
| B. | 若{dn}满足dn=$\frac{{{b_1}•2{b_2}•3{b_3}•…•n{b_n}}}{1•2•3•…•n}$,则{dn}也是等比数列 | |
| C. | 若{dn}满足${d_n}={[{b_1}•(2{b_2})•(3{b_3})•…•(n{b_n})]^{\frac{1}{1+2+…+n}}}$,则{dn}也是等比数列 | |
| D. | 若{dn}满足${d_n}={[{b_1}•{b_2}^2•{b_3}^3•…•{b_n}^n]^{\frac{1}{1+2+…+n}}}$,则{dn}也是等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com