
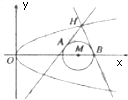
 如图,已知⊙M:(x-4)2+y2=1和抛物线C:y2=2px(p>0,其焦点为F),且$\overrightarrow{FM}$=($\frac{15}{4}$,0,),过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切于A、B两点.
如图,已知⊙M:(x-4)2+y2=1和抛物线C:y2=2px(p>0,其焦点为F),且$\overrightarrow{FM}$=($\frac{15}{4}$,0,),过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切于A、B两点.分析 (1)求得抛物线的焦点和圆的圆心,由条件可得圆心M到抛物线C的焦点的距离为$\frac{15}{4}$,即可得到抛物线方程;
(2)设出H的坐标,由中点坐标公式和直径式圆的方程可得MH为直径的圆,运用和已知圆相减,可得AB的方程,再令x=0,可得截距的表达式,由函数的单调性,即可得到最小值.
解答 解:(1)由题意知⊙M的圆心M的坐标为(4,0),
抛物线C的焦点为($\frac{p}{2}$,0),
由$\overrightarrow{FM}$=($\frac{15}{4}$,0),
圆心M到抛物线C的焦点的距离为$\frac{15}{4}$,即4-$\frac{p}{2}$=$\frac{15}{4}$,解得p=$\frac{1}{2}$,
从而抛物线C的方程为y2=x;
(2)由(1)知,设点H (y02,y0),
则HM的中点($\frac{{{y}_{0}}^{2}+4}{2}$,$\frac{{y}_{0}}{2}$),
以HM为直径的圆为(x-$\frac{{{y}_{0}}^{2}+4}{2}$)2+(y-$\frac{{y}_{0}}{2}$)2=$\frac{({{y}_{0}}^{2}-4)^{2}+{{y}_{0}}^{2}}{4}$…①
⊙M:(x-4)2+y2=1 …②
①-②得:直线AB的方程为(4-y02)x-y0y+4y02-15=0,
令x=0,得直线AB在y轴上的截距为d=$\frac{4{{y}_{0}}^{2}-15}{{y}_{0}}$=4y0-$\frac{15}{{y}_{0}}$(y0≥1)
函数f(y0)=4y0-$\frac{15}{{y}_{0}}$在[1,+∞)为单调递增函数,
∴直线AB在y轴上的截距的最小值为4×1-$\frac{15}{1}$=-11.
点评 本题考查抛物线的方程和性质,主要考查抛物线方程的运用,同时考查圆的方程的运用,由四点共圆和两元方程相减得到相交弦方程是解题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,AB是半径为1的圆的直径,过点A,B分别引弦AD和BE,相交于点C,过点C作CF⊥AB,垂足为点F.已知∠CAB=30°,∠DCB=60°.
如图所示,AB是半径为1的圆的直径,过点A,B分别引弦AD和BE,相交于点C,过点C作CF⊥AB,垂足为点F.已知∠CAB=30°,∠DCB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上的点到它的两个焦点的距离之和为4,以椭圆C的短轴为直径的圆O经过这两个焦点,点A,B分别是椭圆C的左、右顶点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上的点到它的两个焦点的距离之和为4,以椭圆C的短轴为直径的圆O经过这两个焦点,点A,B分别是椭圆C的左、右顶点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
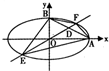 设椭圆中心在坐标原点,A(4,0),B(0,2)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
设椭圆中心在坐标原点,A(4,0),B(0,2)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com