
分析 (Ⅰ)由三角函数中的恒等变换应用化简可得f(x)=sin(2x-$\frac{π}{3}$)+2,由三角函数的周期性及其求法即可得解.
(Ⅱ)由2x-$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z可解得函数f(x)的对称轴;由2x-$\frac{π}{3}$=kπ,k∈Z可解得函数f(x)的对称中心.
解答 解:(Ⅰ)f(x)=2sin(x-$\frac{π}{6}$)cos(x-$\frac{π}{6}$)+2=sin(2x-$\frac{π}{3}$)+2,
可得:函数f(x)的最小正周期T=$\frac{2π}{2}$=π;
(Ⅱ)由2x-$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z可解得函数f(x)的对称轴是:x=$\frac{kπ}{2}$+$\frac{5π}{12}$,k∈Z;
由2x-$\frac{π}{3}$=kπ,k∈Z可解得函数f(x)的对称中心是:($\frac{kπ}{2}$+$\frac{π}{6}$,2)k∈Z;
点评 本题主要考查了三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象和性质,属于基本知识的考查.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | 5 | C. | 3 | D. | $\sqrt{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在四边形ABCD中,AB⊥BC,AB=3,BC=4,△ACD是等边三角形,则$\overrightarrow{AC}•\overrightarrow{BD}$的值为$\frac{7}{2}$.
如图,在四边形ABCD中,AB⊥BC,AB=3,BC=4,△ACD是等边三角形,则$\overrightarrow{AC}•\overrightarrow{BD}$的值为$\frac{7}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
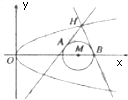 如图,已知⊙M:(x-4)2+y2=1和抛物线C:y2=2px(p>0,其焦点为F),且$\overrightarrow{FM}$=($\frac{15}{4}$,0,),过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切于A、B两点.
如图,已知⊙M:(x-4)2+y2=1和抛物线C:y2=2px(p>0,其焦点为F),且$\overrightarrow{FM}$=($\frac{15}{4}$,0,),过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若{dn}满足dn=$\frac{{{b_1}+2{b_2}+3{b_3}+…+n{b_n}}}{1+2+3+…n}$,则{dn}也是等比数列 | |
| B. | 若{dn}满足dn=$\frac{{{b_1}•2{b_2}•3{b_3}•…•n{b_n}}}{1•2•3•…•n}$,则{dn}也是等比数列 | |
| C. | 若{dn}满足${d_n}={[{b_1}•(2{b_2})•(3{b_3})•…•(n{b_n})]^{\frac{1}{1+2+…+n}}}$,则{dn}也是等比数列 | |
| D. | 若{dn}满足${d_n}={[{b_1}•{b_2}^2•{b_3}^3•…•{b_n}^n]^{\frac{1}{1+2+…+n}}}$,则{dn}也是等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com