
【题目】已知袋中装有红球,黑球共7个,若从中任取两个小球(每个球被取到的可能性相同),其中恰有一个红球的概率为![]() .
.
(1)求袋中红球的个数;
(2)若袋中红球比黑球少,从袋中任取三个球,求三个球中恰有一个红球的概率.
【答案】(1)3个或4个 (2)![]()
【解析】
(1)设袋中红球的个数为x,黑球个数为![]() ,根据分步计数原理求出基本事件总数以及恰有一个红球包含的基本事件数,解方程即可求出答案;
,根据分步计数原理求出基本事件总数以及恰有一个红球包含的基本事件数,解方程即可求出答案;
(2)根据计数原理求出恰有一个红球的基本事件数与基本事件总数,再根据概率计算公式求解即可.
解:(1)设袋中红球的个数为x,黑球个数为![]() ,则:
,则:
总的基本事件个数![]() ,
,
取出一个红球的基本事件个数为![]() ,
,
∴![]() ,化简得
,化简得![]() ,
,
解得![]() 或
或![]() ,
,
∴袋中红球的个数为3个或4个;
(2)由(1)可知袋中有3个红球,4个黑球,
基本事件总数为![]() ,
,
①第一次取红球包含的基本事件数为:![]() ,
,
②第二次取红球包含的基本事件数为:![]() ,
,
③第三次取红球包含的基本事件数为:![]() ,
,
∴所求概率![]() .
.


科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为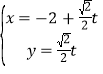 (t为参数).直线
(t为参数).直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:只要
满足:只要![]() ,必有
,必有![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)若![]() 具有性质
具有性质![]() ,且
,且![]() ,
, ![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列, ![]() ,
, ![]() ,
, ![]() 判断
判断![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(3)设![]() 是无穷数列,已知
是无穷数列,已知![]() .求证:“对任意
.求证:“对任意![]() 都具有性质
都具有性质![]() ”的充要条件为“
”的充要条件为“![]() 是常数列”.
是常数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中有5只同型号的灯泡,其中有3只一等品,2只二等品,现在从中依次取出2只,设每只灯泡被取到的可能性都相同,请用“列举法”解答下列问题:
(Ⅰ)求第一次取到二等品,且第二次取到的是一等品的概率;
(Ⅱ)求至少有一次取到二等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,现将
,现将![]() 沿
沿![]() 折到
折到![]() 的位置,连结
的位置,连结![]() ,
,![]() ,如图2
,如图2
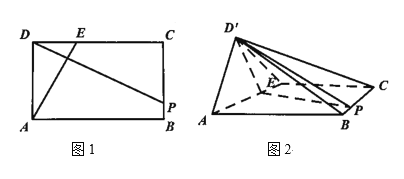
(1)证明:![]() ;
;
(2)记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() .若二面角
.若二面角![]() 为
为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,
,![]() 为圆上任意一点,
为圆上任意一点,![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)记点![]() 的轨迹为曲线
的轨迹为曲线![]() ,点
,点![]() ,
,![]() .若点
.若点![]() 为直线
为直线![]() 上一动点,且
上一动点,且![]() 不在
不在![]() 轴上,直线
轴上,直线![]() 、
、![]() 分别交曲线
分别交曲线![]() 于
于![]() 、
、![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自贡农科所实地考察,研究发现某贫困村适合种植![]() ,
,![]() 两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材
两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材![]() 的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
编号 | 1 | 2 | 3 | 4 | 5 |
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
单价(元/公斤) | 18 | 20 | 23 | 25 | 29 |
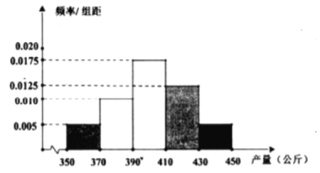
药材![]() 的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:
的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:
(1)若药材![]() 的单价
的单价![]() (单位:元/公斤)与年份编号
(单位:元/公斤)与年份编号![]() 具有线性相关关系,请求出
具有线性相关关系,请求出![]() 关于
关于![]() 的回归直线方程,并估计2020年药材
的回归直线方程,并估计2020年药材![]() 的单价;
的单价;
(2)用上述频率分布直方图估计药材![]() 的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材
的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材![]() 还是药材
还是药材![]() ?并说明理由.
?并说明理由.
参考公式: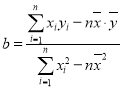 ,
,![]() (回归方程
(回归方程![]() 中)
中)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com