
【题目】若无穷数列![]() 满足:只要
满足:只要![]() ,必有
,必有![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)若![]() 具有性质
具有性质![]() ,且
,且![]() ,
, ![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列, ![]() ,
, ![]() ,
, ![]() 判断
判断![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(3)设![]() 是无穷数列,已知
是无穷数列,已知![]() .求证:“对任意
.求证:“对任意![]() 都具有性质
都具有性质![]() ”的充要条件为“
”的充要条件为“![]() 是常数列”.
是常数列”.
【答案】(1)![]() .(2)
.(2)![]() 不具有性质
不具有性质![]() .(3)见解析.
.(3)见解析.
【解析】试题分析:(1)根据已知条件,得到![]() ,结合
,结合![]() 求解即可.
求解即可.
(2)根据![]() 的公差为
的公差为![]() ,
, ![]() 的公比为
的公比为![]() ,写出通项公式,从而可得
,写出通项公式,从而可得![]() .
.
通过计算![]() ,
, ![]() ,
, ![]() ,
, ![]() ,即知
,即知![]() 不具有性质
不具有性质![]() .
.
(3)从充分性、必要性两方面加以证明,其中必要性用反证法证明.
试题解析:(1)因为![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() .
.
于是![]() ,又因为
,又因为![]() ,解得
,解得![]() .
.
(2)![]() 的公差为
的公差为![]() ,
, ![]() 的公比为
的公比为![]() ,
,
所以![]() ,
, ![]() .
.
![]() .
.
![]() ,但
,但![]() ,
, ![]() ,
, ![]() ,
,
所以![]() 不具有性质
不具有性质![]() .
.
[证](3)充分性:
当![]() 为常数列时,
为常数列时, ![]() .
.
对任意给定的![]() ,只要
,只要![]() ,则由
,则由![]() ,必有
,必有![]() .
.
充分性得证.
必要性:
用反证法证明.假设![]() 不是常数列,则存在
不是常数列,则存在![]() ,
,
使得![]() ,而
,而![]() .
.
下面证明存在满足![]() 的
的![]() ,使得
,使得![]() ,但
,但![]() .
.
设![]() ,取
,取![]() ,使得
,使得![]() ,则
,则
![]() ,
, ![]() ,故存在
,故存在![]() 使得
使得![]() .
.
取![]() ,因为
,因为![]() (
(![]() ),所以
),所以![]() ,
,
依此类推,得![]() .
.
但![]() ,即
,即![]() .
.
所以![]() 不具有性质
不具有性质![]() ,矛盾.
,矛盾.
必要性得证.
综上,“对任意![]() ,
, ![]() 都具有性质
都具有性质![]() ”的充要条件为“
”的充要条件为“![]() 是常数列”.
是常数列”.


科目:高中数学 来源: 题型:
【题目】已知矩阵![]() 将直线l:x+y-1=0变换成直线l′.
将直线l:x+y-1=0变换成直线l′.
(1)求直线l′的方程;
(2)判断矩阵A是否可逆?若可逆,求出矩阵A的逆矩阵A-1;若不可逆,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,点
,点![]() 分别为棱
分别为棱![]() 的中点,
的中点, ![]() 的重心为
的重心为![]() ,直线
,直线![]() 垂直于平面
垂直于平面![]() .
.
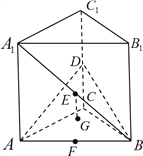
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦.
的余弦.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)将函数![]() 的图像(纵坐标不变)横坐标伸长为原来的
的图像(纵坐标不变)横坐标伸长为原来的![]() 倍,再把整个图像向左平移
倍,再把整个图像向左平移![]() 个单位长度得到
个单位长度得到![]() 的图像.当
的图像.当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)若函数![]() 在
在![]() 内是减函数,求
内是减函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
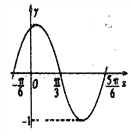
【题目】如图是函数![]() 在区间
在区间![]() 上的图象,为了得到这个函数的图象,只需将y=sinx的图象
上的图象,为了得到这个函数的图象,只需将y=sinx的图象
A. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
B. 向左平移至![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
C. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
D. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数![]() 在区间
在区间![]() 上的图象,为了得到这个函数的图象,只需将y=sinx的图象
上的图象,为了得到这个函数的图象,只需将y=sinx的图象

A. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
B. 向左平移至![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
C. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
D. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
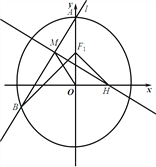
【题目】如图,在直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]()
![]() 的上焦点为
的上焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点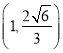 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过椭圆![]() 的上顶点
的上顶点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面的菱形,
的底面的菱形, ![]() ,点E是BC边的中点,AC和DE交于点O,PO
,点E是BC边的中点,AC和DE交于点O,PO ![]() ;
;
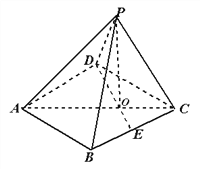
(1)求证: ![]() ;
;
(2)![]() 求二面角P-AD-C的大小。
求二面角P-AD-C的大小。
(3)在(2)的条件下,求异面直线PB与DE所成角的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com