
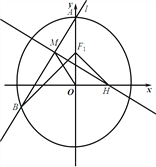
【题目】如图,在直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]()
![]() 的上焦点为
的上焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点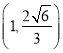 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过椭圆![]() 的上顶点
的上顶点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由椭圆![]() 的离心率为
的离心率为![]() 得
得![]() ,把点
,把点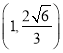 代人椭圆方程,结合
代人椭圆方程,结合![]() ,可求得
,可求得![]() 的值,从而可得椭圆方程;(2)直线
的值,从而可得椭圆方程;(2)直线![]() 的方程为
的方程为![]() ,
,
由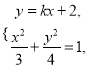 得
得![]() ,根据韦达定理及斜率公式,结合题设
,根据韦达定理及斜率公式,结合题设![]() ,且
,且![]() ,可得
,可得![]() ,求得
,求得![]() 的值即可得结果.
的值即可得结果.
试题解析:(1)因为椭圆![]() 的离心率为
的离心率为![]() ,所以
,所以![]() ,即
,即![]() .
.
又![]() ,得
,得![]() ,即
,即![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为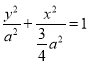 .
.
把点 代人
代人![]() 中,解得
中,解得![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)解法1:设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
由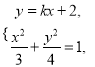 得
得![]() .
.
设![]() ,
, ![]() ,则有
,则有![]() ,
, ![]() ,
,
所以![]() .
.
所以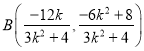
因为![]() ,所以
,所以![]() 在线段
在线段![]() 的中垂线上,
的中垂线上,
所以![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() .
.
设![]() ,又直线
,又直线![]() 垂直
垂直![]() ,所以
,所以![]() ,即
,即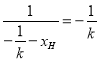 .
.
所以![]() ,即
,即![]() .
.
又![]() ,所以
,所以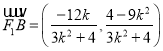 ,
, ![]() .
.
因为![]() ,所以
,所以![]() ,
,
解得![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和数量积公式,属于难题. 利用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】在一个不透明的箱子里装有5个完全相同的小球,球上分别标有数字1、2、3、4、5.甲先从箱子中摸出一个小球,记下球上所标数字后,将该小球放回箱子中摇匀后,乙再从该箱子中摸出一个小球.
(1)若甲、乙两人谁摸出的球上标的数字大谁就获胜(数字相同为平局),求甲获胜的概率;
(2)规定:两人摸到的球上所标数字之和小于6,则甲获胜,否则乙获胜,这样规定公平吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:只要
满足:只要![]() ,必有
,必有![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)若![]() 具有性质
具有性质![]() ,且
,且![]() ,
, ![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列, ![]() ,
, ![]() ,
, ![]() 判断
判断![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(3)设![]() 是无穷数列,已知
是无穷数列,已知![]() .求证:“对任意
.求证:“对任意![]() 都具有性质
都具有性质![]() ”的充要条件为“
”的充要条件为“![]() 是常数列”.
是常数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,点M的坐标为![]() ,曲线C的方程为
,曲线C的方程为![]() ;以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为
;以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为![]() 的直线l经过点M.
的直线l经过点M.
(I)求直线l和曲线C的直角坐标方程:
(II)若P为曲线C上任意一点,直线l和曲线C相交于A,B两点,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,点
,点![]() 分别为棱
分别为棱![]() 的中点,
的中点, ![]() 的重心为
的重心为![]() ,直线
,直线![]() 垂直于平面
垂直于平面![]() .
.
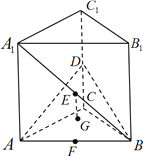
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦.
的余弦.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上存在一点
上存在一点![]()
![]() 到焦点
到焦点![]() 的距离等于
的距离等于![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 两点在
两点在![]() 轴上方),点
轴上方),点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,且
,且![]() ,求△
,求△![]() 的外接圆的方程.
的外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
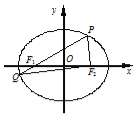
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,P为椭圆上一点(在x轴上方),连结PF1并延长交椭圆于另一点Q,设
(a>b>0)的左、右焦点分别为F1,F2,P为椭圆上一点(在x轴上方),连结PF1并延长交椭圆于另一点Q,设![]() =λ
=λ![]() .
.
(1)若点P的坐标为(1,![]() ),且△PQF2的周长为8,求椭圆C的方程;
),且△PQF2的周长为8,求椭圆C的方程;
(2)若PF2垂直于x轴,且椭圆C的离心率e∈[![]() ,
,![]() ],求实数λ的取值范围.
],求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(I)求棱锥C-ADE的体积;
(II)求证:平面ACE⊥平面CDE;
(III)在线段DE上是否存在一点F,使AF∥平面BCE?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com