考点:数列的求和,等比数列的性质,数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由已知得
,由q为正整数,解得a
1=1,q=2,从而a
n=2
n-1,设数列{b
n}前n项的前n项和为S
n,进而得到S
n=n•2
n-n,由此能求出b
n=(n+1)•2
n-1-1.
(2)由
=
<
=
<
,利用放缩法和等比数列的性质能求出
++…+<2.
解答:
解:(1)∵数列{a
n}是公比为正整数的等比数列,
a
2=2且a
1,
a3+,a
4成等差数列,
∴
,
由q为正整数,解得a
1=1,q=2,
∴a
n=2
n-1,
∵数列{b
n}前n项的“均倒数“为
(n∈N*),
∴
(b1+b2+…+bn)=2a
n-1=2
n-1,
设数列{b
n}前n项的前n项和为S
n,则S
n=n•2
n-n,
∴b
1=1×2-1=1,
n≥2时,b
n=S
n-S
n-1=(n•2
n-n)-[(n-1)•2
n-1-(n-1)]=(n+1)•2
n-1-1,
n=1时,上式成立,
∴b
n=(n+1)•2
n-1-1.
(2)解:∵
=
<
=
<
,
∴
++…+<2(
++…+)
=2×
=2(1-
)<2.
∴
++…+<2.
点评:本题考查数列的通项公式的求法,考查数列的前n项和与2的大小的比较,是中档题,解题时要认真审题,注意等差数列和等比数列的性质的合理运用.



 天天向上口算本系列答案
天天向上口算本系列答案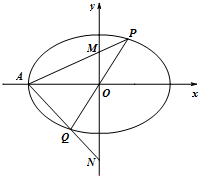 如图,在平面直角坐标系xOy中,离心率为
如图,在平面直角坐标系xOy中,离心率为