
分析 (Ⅰ)由数列{an}的递推公式依次求出a2,a3,a4;
(Ⅱ)根据a2,a3,a4值的结构特点猜想{an}的通项公式,再用数学归纳法①验证n=1成立,②假设n=k时命题成立,证明当n=k+1时命题也成立
解答 解:(Ⅰ)由题意a1=1,a2+a1=$\sqrt{2}$,a3+a2=$\sqrt{3}$-1,a4+a3=2-$\sqrt{2}$
解得:a2=$\sqrt{2}$-1,a3=$\sqrt{3}$-$\sqrt{2}$,a4=2-$\sqrt{3}$
(Ⅱ)猜想:对任意的n∈N*,an=$\sqrt{n}$-$\sqrt{n-1}$,
①当n=1时,由a1=1=$\sqrt{1}$-$\sqrt{1-1}$,猜想成立.
②假设当n=k (k∈N*)时,猜想成立,即
ak=$\sqrt{k}$-$\sqrt{k-1}$
则由ak+1+ak=$\sqrt{k+1}$-$\sqrt{k-1}$,得ak+1=$\sqrt{k+1}$-$\sqrt{k}$,
即当n=k+1时,猜想成立,
由①、②可知,对任意的n∈N*,猜想成立,
即数列{an}的通项公式为an=$\sqrt{n}$-$\sqrt{n-1}$.
点评 本题考查数列递推关系式的应用,数学归纳法证明数列问题的方法,考查逻辑推理能力,计算能力.注意在证明n=k+1时用上假设,化为n=k的形式,属于中档题.


科目:高中数学 来源: 题型:选择题
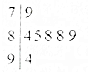 某校高一年级举办歌咏比赛,7位裁判为某班级打出的分数如图茎叶图所示,左边数字表示十位数字,右边数字表示个位数字,则这些数据的中位数是( )
某校高一年级举办歌咏比赛,7位裁判为某班级打出的分数如图茎叶图所示,左边数字表示十位数字,右边数字表示个位数字,则这些数据的中位数是( )| A. | 84 | B. | 85 | C. | 88 | D. | 89 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 楹联社 | B. | 书法社 | ||
| C. | 汉服社 | D. | 条件不足无法判断 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 楹联社 | B. | 书法社 | ||
| C. | 汉服社 | D. | 条件不足无法判断 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,圆C的方程是x2+y2=4.
在平面直角坐标系xOy中,圆C的方程是x2+y2=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com