
 在平面直角坐标系xOy中,圆C的方程是x2+y2=4.
在平面直角坐标系xOy中,圆C的方程是x2+y2=4.分析 (Ⅰ)设直线l的斜率为k,则直线l的方程为y-3=k(x-5),即kx-y-5k+3=0,利用圆心到直线l的距离为$\sqrt{2}$,建立方程,即可求直线l的斜率;
(Ⅱ)先求出M1和点M2的坐标,用两点式求直线PM1 和PM2的方程,根据方程求得他们在y轴上的截距m、n的值,计算mn的值,可得结论.
解答 解:(Ⅰ)由题意,C(0,0),半径r=2,点(5,3)在圆外,
设直线l的斜率为k,则直线l的方程为y-3=k(x-5),即kx-y-5k+3=0,
∵圆心到直线l的距离为$\sqrt{2}$,
∴$\sqrt{2}$=$\frac{|-5k+3|}{\sqrt{1+{k}^{2}}}$,∴k=1或$\frac{7}{23}$,
∴直线l的斜率为1或$\frac{7}{23}$;
(Ⅱ)由于M(x1,y1)、P(x2,y2)是圆O上的两个动点,则可得M1(-x1,-y1)、M2(x1,-y1),且x12+y12=4,x22+y22=4.
根据PM1的方程为$\frac{y+{y}_{1}}{{y}_{2}+{y}_{1}}$=$\frac{x-{x}_{1}}{{x}_{2}+{x}_{1}}$,令x=0求得y=m=$\frac{{x}_{1}{y}_{2}-{x}_{2}{y}_{1}}{{x}_{2}+{x}_{1}}$.
根据PM2的方程为$\frac{y+{y}_{1}}{{y}_{2}+{y}_{1}}$=$\frac{x-{x}_{1}}{{x}_{2}-{x}_{1}}$,令x=0求得y=n=$\frac{-{x}_{1}{y}_{2}-{x}_{2}{y}_{1}}{{x}_{2}-{x}_{1}}$
∴mn=$\frac{{x}_{1}{y}_{2}-{x}_{2}{y}_{1}}{{x}_{2}+{x}_{1}}$•$\frac{-{x}_{1}{y}_{2}-{x}_{2}{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{{{x}_{2}}^{2}(4-{{x}_{1}}^{2})-{{x}_{1}}^{2}(4-{{x}_{2}}^{2})}{{{x}_{2}}^{2}-{{x}_{1}}^{2}}$=4为定值.
点评 本题主要考查直线和圆相交的性质,点到直线的距离公式,用两点式求直线的方程、求直线在y轴上的截距,属于中档题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈(0,$\frac{π}{4}$),sinx>cosx”的否定是“?x0∈(0,$\frac{π}{4}$),sinx<cosx” | |
| B. | 函数y=sinx+cosx的最大值是$\sqrt{2}$ | |
| C. | 已知a,b为实数,则a+b=0的充要条件是$\frac{a}{b}$=-1 | |
| D. | 函数y=2cos2(x-$\frac{π}{4}$)-1既不是奇函数,也不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
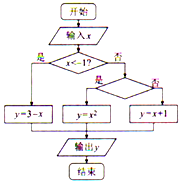 已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )
已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )| A. | x≥1? | B. | x≥-1? | C. | -1≤x≤2? | D. | x≤1? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com