
| A. | 命题“?x∈(0,$\frac{π}{4}$),sinx>cosx”的否定是“?x0∈(0,$\frac{π}{4}$),sinx<cosx” | |
| B. | 函数y=sinx+cosx的最大值是$\sqrt{2}$ | |
| C. | 已知a,b为实数,则a+b=0的充要条件是$\frac{a}{b}$=-1 | |
| D. | 函数y=2cos2(x-$\frac{π}{4}$)-1既不是奇函数,也不是偶函数 |
分析 写出特称命题的否定判断A;求出函数的值域判断B;由充分必要条件的判定方法判断C;利用倍角公式化简后由函数奇偶性的定义判断D.
解答 解:命题“?x∈(0,$\frac{π}{4}$),sinx>cosx”的否定是“?x0∈(0,$\frac{π}{4}$),sinx≤cosx”,故A错误;
∵y=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$),∴函数y=sinx+cosx的最大值是$\sqrt{2}$,故B正确;
a,b为实数,若a=b=0,满足a+b=0,不能得到$\frac{a}{b}$=-1,故C错误;
函数y=2cos2(x-$\frac{π}{4}$)-1=cos2(x-$\frac{π}{4}$)=cos($\frac{π}{2}-2x$)=sin2x,是奇函数,故D错误.
故选:B.
点评 本题考查命题的真假判断与应用,考查三角函数的性质及值域的求法,考查特称命题的否定及充分必要条件的判定方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{7}{2}$ | B. | $\frac{7}{2}$ | C. | $-\frac{9}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
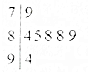 某校高一年级举办歌咏比赛,7位裁判为某班级打出的分数如图茎叶图所示,左边数字表示十位数字,右边数字表示个位数字,则这些数据的中位数是( )
某校高一年级举办歌咏比赛,7位裁判为某班级打出的分数如图茎叶图所示,左边数字表示十位数字,右边数字表示个位数字,则这些数据的中位数是( )| A. | 84 | B. | 85 | C. | 88 | D. | 89 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
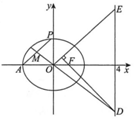 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为为$\frac{1}{2}$,F为椭圆C的右焦点A(-a,0),|AF|=3.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为为$\frac{1}{2}$,F为椭圆C的右焦点A(-a,0),|AF|=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 6 | C. | 8.5 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,圆C的方程是x2+y2=4.
在平面直角坐标系xOy中,圆C的方程是x2+y2=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com