
| A. | 2 | B. | 6 | C. | 8.5 | D. | 10 |
分析 确定商场该年对该商品征收的总管理费的函数解析式,再根据第二年商场在A种产品经营中收取的管理费不少于14万元,建立不等式,即可求得x的最大值.
解答 解:依题意,第二年该商品年销售量为(11.8-x)万件,年销售收入为$\frac{70•x%}{1-x%}$(11.8-x)万元,?
则商场该年对该商品征收的总管理费为$\frac{70•x%}{1-x%}$(11.8-x)x%(万元).
故所求函数为:y=$\frac{7}{100-x}$(118-10x)x(x>0).
令$\frac{7}{100-x}$(118-10x)x≥14,化简得x2-12x+20≤0,即(x-2)(x-10)≤0,解得2≤x≤10.?
∴x的最大值是10
故选:D
点评 本题考查的知识点是函数的最值及其几何意义,函数模型的构建,解题的关键是根据题意构建函数,同时考查解不等式,属于中档题


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 5或-3 | B. | 2或6 | C. | 5或3 | D. | $\sqrt{5}$或$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 考前预估难度Pi | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
| 题号 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | × | √ | √ | √ | √ |
| 2 | √ | √ | √ | √ | × |
| 3 | √ | √ | √ | √ | × |
| 4 | √ | √ | √ | × | × |
| 5 | √ | √ | √ | √ | √ |
| 6 | √ | × | × | √ | × |
| 7 | × | √ | √ | √ | × |
| 8 | √ | × | × | × | × |
| 9 | √ | √ | √ | × | × |
| 10 | √ | √ | √ | √ | × |
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 实测答对人数 | |||||
| 实测难度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈(0,$\frac{π}{4}$),sinx>cosx”的否定是“?x0∈(0,$\frac{π}{4}$),sinx<cosx” | |
| B. | 函数y=sinx+cosx的最大值是$\sqrt{2}$ | |
| C. | 已知a,b为实数,则a+b=0的充要条件是$\frac{a}{b}$=-1 | |
| D. | 函数y=2cos2(x-$\frac{π}{4}$)-1既不是奇函数,也不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
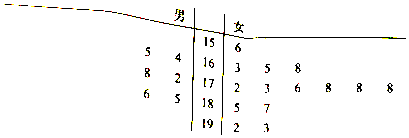
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}+\frac{1}{b}$有最大值4 | B. | $\sqrt{ab}$有最小值 $\frac{1}{2}$ | C. | $\sqrt{a}+\sqrt{b}$有最大值$\sqrt{2}$ | D. | a2+b2有最小值$\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}$或-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com