
分析 (Ⅰ)数列{an}满足a1=1,an+1+an=$\sqrt{n+1}$-$\sqrt{n-1}$,n∈N*.a2=$\sqrt{2}$-1,同理可得:a3=$\sqrt{3}$$-\sqrt{2}$,a4=$\sqrt{4}-\sqrt{3}$,归纳猜想:an.
(Ⅱ)由(Ⅰ)得:S1=a1=1,S2=a1+a2=$\sqrt{2}$,S3=S2+a3=$\sqrt{3}$,假设数列{Sn}是等差数列,则S1,S2,S3成等差数列,推出矛盾.
解答 解:(Ⅰ)数列{an}满足a1=1,an+1+an=$\sqrt{n+1}$-$\sqrt{n-1}$,n∈N*.
∴a2=$\sqrt{2}$-1,同理可得:a3=$\sqrt{3}$$-\sqrt{2}$,a4=$\sqrt{4}-\sqrt{3}$,…,
归纳猜想:an=$\sqrt{n}$-$\sqrt{n-1}$.
(Ⅱ)证明:由(Ⅰ)得:S1=a1=1,S2=a1+a2=$\sqrt{2}$,S3=S2+a3=$\sqrt{3}$,
假设数列{Sn}是等差数列,
则S1,S2,S3成等差数列,
所以S1+S3=2S2,
即1+$\sqrt{3}$=2$\sqrt{2}$,
两边平方得$\sqrt{3}$=2
这显然不成立,所以假设错误,所以数列{Sn}不是等差数列.
点评 本题考查了数列递推关系、等差数列的通项公式、反证法,考查了推理能力与计算能力,属于中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 1 | 2 | 3 | 4 |
| f(x) | 2 | 3 | 4 | 1 |
| f′(x) | 3 | 4 | 2 | 1 |
| g(x) | 3 | 1 | 4 | 2 |
| g′(x) | 2 | 4 | 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
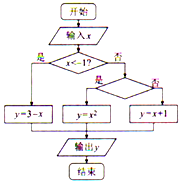 已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )
已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )| A. | x≥1? | B. | x≥-1? | C. | -1≤x≤2? | D. | x≤1? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2n-1)2 | B. | 4n-1 | C. | $\frac{{4}^{n}-1}{3}$ | D. | $\frac{{4}^{n+1}-4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com