
分析 (Ⅰ)由余弦定理得c2-2c-8=0,由此能求出c.
(Ⅱ)法一由正弦定理得b=4sinB,c=4sinC,从而b+c=4(sinB+sinC)=4$\sqrt{3}$sin(B+$\frac{π}{6}$),由$A=\frac{π}{3}$,能求出b+c的取值范围.
法二:由余弦定理得$12={b^2}+{c^2}-2bc•cos\frac{π}{3}$=(b+c)2-3bc$≥{(b+c)^2}-3×{(\frac{b+c}{2})^2}$,由此能求出b+c的取值范围.
解答 解:(Ⅰ)∵$a=2\sqrt{3}$,$A=\frac{π}{3}$,b=2,
∴由余弦定理a2=b2+c2-2bccosA,
得c2-2c-8=0….(4分)
即(c-4)(c+2)=0. 又c>0,
故取c=4. ….(7分)
(Ⅱ)(方法一)由正弦定理得$b=\frac{a}{sinA}•sinB=4sinB$,
同理c=4sinC. ….(9分)
b+c=4(sinB+sinC)=$4[sinB+sin(\frac{2π}{3}-B)]$=$4(sinB+\frac{{\sqrt{3}}}{2}cosB+\frac{1}{2}sinB)$=$4\sqrt{3}sin(B+\frac{π}{6})$. ….(12分)
由$A=\frac{π}{3}$知,$0<B<\frac{2π}{3}$,$\frac{π}{6}<B+\frac{π}{6}<\frac{5π}{6}$.
得$\frac{1}{2}<sin(B+\frac{π}{6})≤1$.
所以$2\sqrt{3}<b+c≤4\sqrt{3}$,
即b+c的取值范围是$(2\sqrt{3,}4\sqrt{3}]$….(15分)
(方法二)由余弦定理得$12={b^2}+{c^2}-2bc•cos\frac{π}{3}$=(b+c)2-3bc$≥{(b+c)^2}-3×{(\frac{b+c}{2})^2}$….(10分)
解得$b+c≤4\sqrt{3}$.
又$b+c>a=2\sqrt{3}$.
所以b+c的取值范围是$(2\sqrt{3},4\sqrt{3}]$. ….(15分)
点评 本题考查三角形边长、两边和取值范围、正弦定理、余弦定理等基础知识,考查推理论证能力、数据处理能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
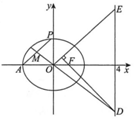 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为为$\frac{1}{2}$,F为椭圆C的右焦点A(-a,0),|AF|=3.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为为$\frac{1}{2}$,F为椭圆C的右焦点A(-a,0),|AF|=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
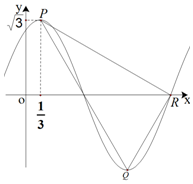 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )| A. | $f(x)=\sqrt{3}sin(\frac{π}{2}x+\frac{π}{3})$ | B. | $f(x)=\sqrt{3}sin(\frac{π}{2}x-\frac{π}{6})$ | ||
| C. | $f(x)=\sqrt{3}sin(\frac{2π}{3}x+\frac{5π}{18})$ | D. | $f(x)=\sqrt{3}sin(πx+\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 楹联社 | B. | 书法社 | ||
| C. | 汉服社 | D. | 条件不足无法判断 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2-ln2 | B. | 2ln2-$\frac{1}{2}$ | C. | 2+ln2 | D. | 2ln2+$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com