
分析 用数学归纳法证明:(1)当n=1时,去证明等式成立;(2)假设当n=k时,等时成立,用上归纳假设后,去证明当n=k+1时,等式也成立即可.
解答 解:证明:(1)当n=1时,1=1,等式成立.
(2)假设当n=k时,有1+2+3+…+k=$\frac{1}{2}$k(k+1)成立.
那么,当n=k+1时,
1+2+3+…+k+k+1=$\frac{1}{2}$k(k+1)+(k+1)
=$\frac{1}{2}$(k+1)(k+2),
=$\frac{1}{2}$(k+1)[(k+1)+1],
∴当n=k+1时等式成立,
∴对任意的n∈N*,等式都成立.
点评 本题的考点是数学归纳法,主要考查数学归纳法的第二步,在假设的基础上,n=k+1时等式左边增加的项,关键是搞清n=k时,等式左边的规律,从而使问题得解,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4cos5-2sin5 | B. | -2sin5-4cos5 | C. | 2sin5-4cos5 | D. | -2sin5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
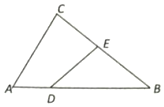 如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=3AD,BC=2BE.
如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=3AD,BC=2BE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com