
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,
,![]() ,且
,且![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)见解析;(2)余弦值为![]() .
.
【解析】分析:(1)由四边形![]() 为菱形,得对角线
为菱形,得对角线![]() ,由侧面
,由侧面![]() 底面
底面![]() ,
,![]() , 得到
, 得到![]() 侧面
侧面![]() ,从而
,从而![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ;
;
(2)由题意易知![]() 为等边三角形,以
为等边三角形,以![]() 点为坐标原点,
点为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 平行
平行![]() 的直线为
的直线为![]() ,建立空间直角坐标系,分别求出平面
,建立空间直角坐标系,分别求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,由此能求出二面角
的法向量,由此能求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
详解:(Ⅰ)由已知侧面![]() 底面
底面![]() ,
,![]() ,
, ![]() 底面
底面![]() ,
,
得到![]() 侧面
侧面![]() ,
,
又因为![]()
![]() 侧面
侧面![]() ,所以
,所以![]() ,
,
又由已知![]() ,侧面
,侧面![]() 为菱形,所以对角线
为菱形,所以对角线![]() ,
,
即![]() ,
,![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)设线段![]() 的中点为
的中点为![]() 点,连接
点,连接![]() ,
,![]() ,因为
,因为![]() ,易知
,易知![]() 为等边三角形,中线
为等边三角形,中线![]()
![]()
![]() ,由(Ⅰ)
,由(Ⅰ)![]() 侧面
侧面![]() ,所以
,所以![]() ,得到
,得到![]() 平面
平面![]() ,
,![]() 即为
即为![]() 与平面
与平面![]() 所成的角,
所成的角,![]() ,
,![]() ,
,![]() ,
, ![]() ,得到
,得到![]() ;
;
以![]() 点为坐标原点,
点为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 平行
平行![]() 的直线为
的直线为![]() ,建立空间直角坐标系,
,建立空间直角坐标系,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由(Ⅰ)知平面![]() 的法向量为
的法向量为![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,
,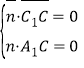 ,
,
解得![]() ,
,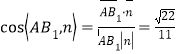 ,
,
二面角![]() 为钝二面角,故余弦值为
为钝二面角,故余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像与
的图像与![]() 轴的相邻两交点的坐标分别为
轴的相邻两交点的坐标分别为![]() ,
,![]() ,且当
,且当![]() 时,
时,![]() 有最小值.
有最小值.
(1)求函数![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)将![]() 的图像向右平移
的图像向右平移![]() 个单位,再将所得图像的横坐标伸长为原来的
个单位,再将所得图像的横坐标伸长为原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图像,若关于
的图像,若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个解,求
上有两个解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:在平面四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() (如图1),若将
(如图1),若将![]() 沿对角线BD折叠,使
沿对角线BD折叠,使![]() (如图2).请在图2中解答下列问题.
(如图2).请在图2中解答下列问题.
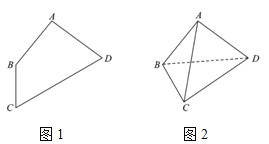
(1)证明:![]() ;
;
(2)求三棱锥![]() 的高.
的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.

(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把一个圆分成n(n≥2)个扇形,依次记为![]() ,每一扇形都可用红、白、蓝三种不同颜色的任一种涂色,要求相邻的扇形的颜色互不相同,问有多少种涂色法?
,每一扇形都可用红、白、蓝三种不同颜色的任一种涂色,要求相邻的扇形的颜色互不相同,问有多少种涂色法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com