
【题目】已知:在平面四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() (如图1),若将
(如图1),若将![]() 沿对角线BD折叠,使
沿对角线BD折叠,使![]() (如图2).请在图2中解答下列问题.
(如图2).请在图2中解答下列问题.
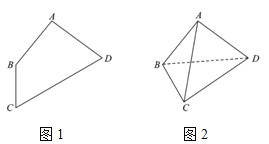
(1)证明:![]() ;
;
(2)求三棱锥![]() 的高.
的高.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)在图1中,根据平面几何知识可得BC=1且∠CBD=90°,在图2中可以得到AC2=AB2+CB2,从而可证明BC⊥平面ABD从而可证明结论.
(2)由(1)有![]() ,用等体积法有
,用等体积法有![]() .
.
证明:法1:由左图知,![]()
在△BDC中,∠CBD=135°-45°=90°,
∠BDC=75°-45°=30°,
![]() ,所以BC=1,
,所以BC=1,
又在右图中,因为AC![]() ,AB=AD
,AB=AD![]() ,所以AC2=AB2+CB2
,所以AC2=AB2+CB2
所以BC⊥AB
又因为∠CBD=90°,所以BC⊥平面ABD
所以BC⊥AD
法2:如右图,设BD的中点为O,连结A0,CO,因为∠A=90°,AB=AD![]()
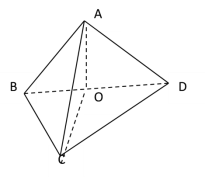
则![]()
由左图知,在△BDC中,∠CBD=135°-45°=90°
∠BDC=75°-45°=30°,所以BC=1,所以![]()
又因为AC![]() ,所以AC2=AO2+CO2
,所以AC2=AO2+CO2
所以AO⊥CO,所以AO⊥平面BCD,所以平面ABD⊥平面BCD,又∠CBD=90°
所以BC⊥平面ABD, 所以BC⊥AD
(2)因为AB=AD![]() ,AC
,AC![]() ,CD2=BC2+BD2=4
,CD2=BC2+BD2=4
所以CD2=AC2+AD2,所以AC⊥AD
设三棱锥B-ADC的高为h,则
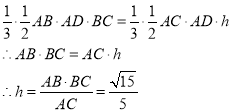


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 是一个棱长为2的空心蔬菜大棚,由8个钢结构(地面没有)组合搭建而成的,四个侧面及顶上均被可采光的薄膜覆盖,已知
是一个棱长为2的空心蔬菜大棚,由8个钢结构(地面没有)组合搭建而成的,四个侧面及顶上均被可采光的薄膜覆盖,已知![]() 为柱
为柱![]() 上一点(不在点
上一点(不在点![]() 、
、![]() 处),
处),![]() (
(![]() ),菜农需要在地面正方形
),菜农需要在地面正方形![]() 内画出一条曲线
内画出一条曲线![]() 将菜地分隔为两个不同的区域来种植不同品种的蔬菜以加强管理,现已知点
将菜地分隔为两个不同的区域来种植不同品种的蔬菜以加强管理,现已知点![]() 为地面正方形
为地面正方形![]() 内的曲线
内的曲线![]() 上任意一点,设
上任意一点,设![]() 、
、![]() 分别为在
分别为在![]() 点处观测
点处观测![]() 和
和![]() 的仰角.
的仰角.
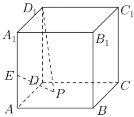
(1)若![]() ,请说明曲线
,请说明曲线![]() 是何种曲线,为什么?
是何种曲线,为什么?
(2)若![]() 为柱
为柱![]() 的中点,且
的中点,且![]() 时,请求出点
时,请求出点![]() 所在区域的面积.
所在区域的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 是抛物线
是抛物线![]() :
:![]() 的焦点,动直线
的焦点,动直线![]() 过点
过点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() ,
,![]() 两点.当直线
两点.当直线![]() 变化时,
变化时,![]() 的最小值为4.
的最小值为4.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过点![]() ,
,![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 与
与![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,求证:
,求证:![]() 与
与![]() 的面积之比为定值(
的面积之比为定值(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设P、M、N分别是正方体的棱![]() ,AD,AB上非顶点的任意点.
,AD,AB上非顶点的任意点.
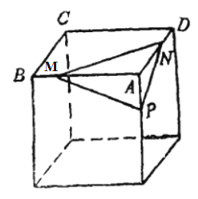
①![]() 的外心必在
的外心必在![]() 的某一边上;
的某一边上;
②![]() 的外心必在
的外心必在![]() 的内部;
的内部;
③![]() 的垂心必是点A在平面PMN上的射影;
的垂心必是点A在平面PMN上的射影;
④若线段AP、AM、AN的长分别为a、b、c,则![]() .其中( ).
.其中( ).
A. 只有①、④正确.
B. 只有③、④正确.
C. 只有②、③、④正确.
D. 只有②、③正确.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了丰富学生的课外文化生活,某中学积极探索开展课外文体活动的新途径及新形式,取得了良好的效果.为了调查学生的学习积极性与参加文体活动是否有关,学校对200名学生做了问卷调查,列联表如下:
参加文体活动 | 不参加文体活动 | 合计 | |
学习积极性高 | 80 | ||
学习积极性不高 | 60 | ||
合计 | 200 |
已知在全部200人中随机抽取1人,抽到学习积极性不高的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.9%的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人,再从所选出的5人中随机选取2人,求至少有1人学习积极性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
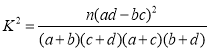 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com