
如图,在三棱锥S—ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°。
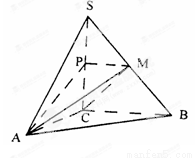
(1)求证:平面MAP⊥平面SAC。
(2)求二面角M—AC—B的平面角的正切值;
(1)详见解析,(2)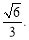
【解析】
试题分析:(1)要证面面垂直,需证线面垂直 观察的证明方向为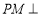 面
面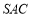 由
由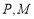 是
是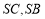 的中点,易得
的中点,易得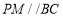 ,所以证明方向转为
,所以证明方向转为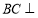 平面
平面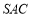 ,又
,又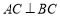 ,所以只需找出
,所以只需找出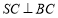 ,而这由
,而这由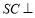 平面
平面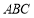 可得,(2)求二面角,关键问题在作出二面角的平面角 作二面角的平面角方法主要是找出二面角棱的垂面,而这在题中易得,即
可得,(2)求二面角,关键问题在作出二面角的平面角 作二面角的平面角方法主要是找出二面角棱的垂面,而这在题中易得,即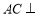 平面
平面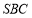 异面直线所成角关键找平移,所以过点
异面直线所成角关键找平移,所以过点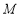 作
作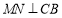 于
于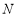 点,使直线
点,使直线 平移到直线
平移到直线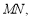 在把空间角转化为平面角后,只需找三角形解出即可
在把空间角转化为平面角后,只需找三角形解出即可
试题解析:解(1)因为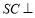 平面
平面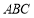 ,
,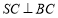 ,又因为
,又因为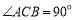
所以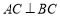 ,
,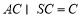 ,
,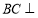 平面
平面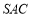 ,
,
又因为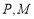 是
是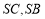 的中点
的中点
所以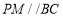 ,
,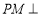 面
面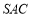 ,所以面
,所以面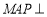 面
面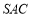 5分
5分
(2)因为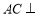 平面
平面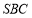 ,
,
所以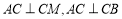 ,从而
,从而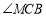 为二面角
为二面角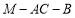 的平面角,
的平面角,
因为直线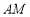 与直线
与直线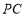 所成的角为
所成的角为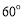
所以过点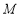 作
作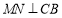 于
于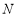 点,连结
点,连结
则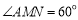 在
在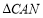 中,由勾股定理得
中,由勾股定理得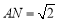
在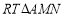 中,
中,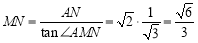
在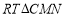 中,
中,
考点:面面垂直判定,二面角,直线与直线所成角


科目:高中数学 来源:2016届山东省文登市高一上学期期末统考数学试卷(解析版) 题型:选择题
一个几何体的三视图如下图所示,这个几何体可能是一个( )

A.三棱锥 B.底面不规则的四棱锥
C.三棱柱 D.底面为正方形的四棱锥
查看答案和解析>>
科目:高中数学 来源:2016届安徽涡阳四中蒙城六中高一上学期期末联考数学卷(解析版) 题型:填空题
等腰梯形 ,上底
,上底 ,腰
,腰 ,下底
,下底 ,以下底所在直线为x轴,则由斜二测画法画出的直观图
,以下底所在直线为x轴,则由斜二测画法画出的直观图 的面积为_______.
的面积为_______.
查看答案和解析>>
科目:高中数学 来源:2016届安徽涡阳四中蒙城六中高一上学期期末联考数学卷(解析版) 题型:选择题
如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为( )
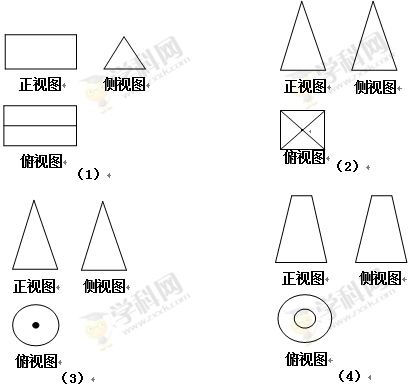
A.三棱台、三棱柱、圆锥、圆台 B.三棱台、三棱锥、圆锥、圆台
C.三棱柱、正四棱锥、圆锥、圆台 D.三棱柱、三棱台、圆锥、圆台
查看答案和解析>>
科目:高中数学 来源:2016届宁夏高一上学期期末考试数学试卷(解析版) 题型:填空题
下面给出五个命题:
①已知平面 //平面
//平面 ,
, 是夹在
是夹在 间的线段,若
间的线段,若 //
// ,则
,则 ;
;
② 是异面直线,
是异面直线, 是异面直线,则
是异面直线,则 一定是异面直线;
一定是异面直线;
③三棱锥的四个面可以都是直角三角形。
④平面 //平面
//平面 ,
, ,
, //
// ,则
,则 ;
;
⑤三棱锥中若有两组对棱互相垂直,则第三组对棱也一定互相垂直;
其中正确的命题编号是 (写出所有正确命题的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com