
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)求出lnx<$\frac{1}{2}$x-$\frac{1}{2x}$,令x=1+$\frac{1}{{n}^{2}}$(n≥2),得到ln(1+$\frac{1}{{n}^{2}}$)<$\frac{1}{2}$($\frac{1}{n-1}$-$\frac{1}{n+1}$),累加即可证明结论.
解答 解:(Ⅰ)函数f(x)的定义域是(0,+∞),
f′(x)=$\frac{-{ax}^{2}+x-a}{{x}^{2}}$,令h(x)=-ax2+x-a,
记△=1-4a2,当△≤0时,得a≥$\frac{1}{2}$,
若a≥$\frac{1}{2}$,则-ax2+x-a≤0,f′(x)≤0,
此时函数f(x)在(0,+∞)递减,
当0<a<$\frac{1}{2}$时,由-ax2+x-a=0,解得:x1=$\frac{1+\sqrt{1-{4a}^{2}}}{2a}$,x2=$\frac{1-\sqrt{1-{4a}^{2}}}{2a}$,
显然x1>x2>0,故此时函数f(x)在($\frac{1-\sqrt{1-{4a}^{2}}}{2a}$,$\frac{1+\sqrt{1-{4a}^{2}}}{2a}$)递增,
在(0,$\frac{1-\sqrt{1-{4a}^{2}}}{2a}$)和($\frac{1+\sqrt{1-{4a}^{2}}}{2a}$,+∞)递减;
综上,0<a<$\frac{1}{2}$时,函数f(x)在($\frac{1-\sqrt{1-{4a}^{2}}}{2a}$,$\frac{1+\sqrt{1-{4a}^{2}}}{2a}$)递增,
在(0,$\frac{1-\sqrt{1-{4a}^{2}}}{2a}$)和($\frac{1+\sqrt{1-{4a}^{2}}}{2a}$,+∞)递减,
a≥$\frac{1}{2}$时,函数f(x)在(0,+∞)递减;
(Ⅱ)证明:令a=$\frac{1}{2}$,由(Ⅰ)中讨论可得函数f(x)在区间(0,+∞)递减,
又f(1)=0,从而当x∈(1,+∞)时,有f(x)<0,即lnx<$\frac{1}{2}$x-$\frac{1}{2x}$,
令x=1+$\frac{1}{{n}^{2}}$(n≥2),
则ln(1+$\frac{1}{{n}^{2}}$)<$\frac{1}{2}$(1+$\frac{1}{{n}^{2}}$)-$\frac{1}{2(1+\frac{1}{{n}^{2}})}$=$\frac{1+{2n}^{2}}{{2n}^{2}{(n}^{2}+1)}$
=$\frac{1}{2}$($\frac{1}{{n}^{2}}$+$\frac{1}{{n}^{2}+1}$)<$\frac{1}{{n}^{2}-1}$=$\frac{1}{2}$($\frac{1}{n-1}$-$\frac{1}{n+1}$),
从而:ln(1+$\frac{1}{{2}^{2}}$)+ln(1+$\frac{1}{{3}^{2}}$)+ln(1+$\frac{1}{{4}^{2}}$)+…+ln(1+$\frac{1}{{n}^{2}}$)
<$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{n-3}$-$\frac{1}{n-1}$+$\frac{1}{n-2}$-$\frac{1}{n}$+$\frac{1}{n-1}$-$\frac{1}{n+1}$)
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n}$-$\frac{1}{n+1}$)<$\frac{1}{2}$(1+$\frac{1}{2}$)=$\frac{3}{4}$,
则有ln(1+$\frac{1}{{2}^{2}}$)+ln(1+$\frac{1}{{3}^{2}}$)+ln(1+$\frac{1}{{4}^{2}}$)+…+ln(1+$\frac{1}{{n}^{2}}$)<$\frac{3}{4}$,
可得(1+$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{3}^{2}}$)(1+$\frac{1}{{4}^{2}}$)…(1+$\frac{1}{{n}^{2}}$)<e${\;}^{\frac{3}{4}}$(n∈N*,n≥2).
点评 本题考查了函数的单调性问题,考查不等式的证明以及导数的应用,是一道中档题.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{10}({x}_{i}-\overline{x})^{2}$ | $\sum_{i=1}^{10}({w}_{i}-\overline{w})^{2}$ | $\sum_{i=1}^{10}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$ | $\sum_{i=1}^{10}({w}_{i}-\overline{w})({y}_{i}-\overline{y})$ |
| 1.63 | 37.8 | 0.89 | 5.15 | 0.92 | -20.6 | 18.40 |
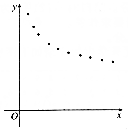 (Ⅰ)根据散点图判断,$\widehat{y}$=$\widehat{a}$+$\widehat{b}$x与$\widehat{y}$=$\widehat{c}$+$\frac{\widehat{d}}{x}$哪一个更适宜作价格y关于时间x的回归方程类型?(不必说明理由)
(Ⅰ)根据散点图判断,$\widehat{y}$=$\widehat{a}$+$\widehat{b}$x与$\widehat{y}$=$\widehat{c}$+$\frac{\widehat{d}}{x}$哪一个更适宜作价格y关于时间x的回归方程类型?(不必说明理由)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±512 | B. | 512 | C. | ±1024 | D. | 1024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2或$\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com