
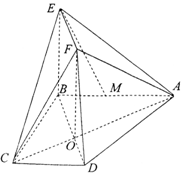
 如图所示,梯形ABCD两条对角线AC,BD的交点为O,AB=2CD,四边形OBEF为矩形,M为线段AB上一点,AM=2MB.
如图所示,梯形ABCD两条对角线AC,BD的交点为O,AB=2CD,四边形OBEF为矩形,M为线段AB上一点,AM=2MB.分析 (Ⅰ)过点O作ON∥AB,交AD于点N,连接MN,FN,证明:EM∥NF,即可证明EM∥平面ADF;
(Ⅱ)证明EF⊥平面ACF,EF⊥AC,即可证明AC⊥BD.
解答 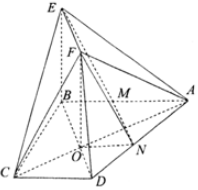 (Ⅰ)证明:过点O作ON∥AB,交AD于点N,连接MN,FN,
(Ⅰ)证明:过点O作ON∥AB,交AD于点N,连接MN,FN,
∵ON∥AB,AB=2CD,
∴$\frac{ON}{AB}$=$\frac{OD}{BD}$=$\frac{1}{3}$,
∵AM=2MB,
∴ON=BM,∴OBMN是平行四边形,
∵四边形OBEF为矩形,
∴EMNF是平行四边形,
∴EM∥NF,
∵EM?平面ADF,NF?平面ADF,
∴EM∥平面ADF;
(Ⅱ)∵四边形OBEF为矩形,
∴EF⊥OF,
∵EF⊥CF,OF∩CF=F,
∴EF⊥平面ACF,
∴EF⊥AC,
∵EF∥BD,∴AC⊥BD.
点评 本题考查线面平行的判定,考查线面垂直的判定,考查学生分析解决问题的能力,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{{2\sqrt{3}}}{3}$) | B. | (1,2) | C. | (2,+∞) | D. | ($\frac{{2\sqrt{3}}}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com