
| ����� | 0��5 | 1��6 | 2��7 | 3��8 | 4��9 |
| ������ | ����һ | ���ڶ� | ������ | ������ | ������ |
���� ��I�����¼�M��ʾ�����ڶ�ֻ��һ���������������¼�N��ʾ�����ڶ�û���������������ɵã�P��M��=${∁}_{2}^{1}����\frac{1}{2}��^{2}����\frac{1}{3}��^{2}$+${∁}_{2}^{1}��\frac{2}{3}��\frac{1}{3}����\frac{1}{2}��^{2}$=$\frac{6}{36}$��P��N��=$��\frac{1}{2}��^{2}����\frac{1}{3}��^{2}$=$\frac{1}{36}$���ɵøù�˾�����ڶ�������2�����������ĸ���P=1-P��M��-P��N����
��II���εĿ���ȡֵΪ0��1��2��3��4������������¼��������¼����ŵ���ʼ��㹫ʽ���ɵó���
��� �⣺��I�����¼�M��ʾ�����ڶ�ֻ��һ���������������¼�N��ʾ�����ڶ�û��������������
��P��M��=${∁}_{2}^{1}����\frac{1}{2}��^{2}����\frac{1}{3}��^{2}$+${∁}_{2}^{1}��\frac{2}{3}��\frac{1}{3}����\frac{1}{2}��^{2}$=$\frac{6}{36}$��P��N��=$��\frac{1}{2}��^{2}����\frac{1}{3}��^{2}$=$\frac{1}{36}$��
��ù�˾�����ڶ�������2�����������ĸ���P=1-P��M��-P��N��=$\frac{29}{36}$��
��II���εĿ���ȡֵΪ0��1��2��3��4��
��P����=0��=$��\frac{1}{2}��^{2}����\frac{1}{3}��^{2}$=$\frac{1}{36}$��
P����=1��=${∁}_{2}^{1}����\frac{1}{2}��^{2}����\frac{1}{3}��^{2}$+${∁}_{2}^{1}��\frac{2}{3}��\frac{1}{3}����\frac{1}{2}��^{2}$=$\frac{6}{36}$��
P����=2��=$��\frac{2}{3}��^{2}����\frac{1}{2}��^{2}$+${∁}_{2}^{1}��\frac{2}{3}��\frac{1}{3}��{∁}_{2}^{1}$��$��\frac{1}{2}��^{2}$+$��\frac{1}{2}��^{2}����\frac{1}{3}��^{2}$=$\frac{13}{36}$��
P����=3��=$��\frac{2}{3}��^{2}��{∁}_{2}^{1}����\frac{1}{2}��^{2}$+${∁}_{2}^{1}��\frac{2}{3}��\frac{1}{3}����\frac{1}{2}��^{2}$=$\frac{12}{36}$��
P����=4��=$��\frac{2}{3}��^{2}����\frac{1}{2}��^{2}$=$\frac{4}{36}$���εķֲ��У�
����Ϊ
| �� | 0 | 1 | 2 | 3 | 4 |
| p | $\frac{1}{36}$ | $\frac{6}{36}$ | $\frac{13}{36}$ | $\frac{12}{36}$ | $\frac{4}{36}$ |
���� ���⿼���������������¼��������¼����ŵ���ʼ��㹫ʽ����������ķֲ�������ѧ������������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
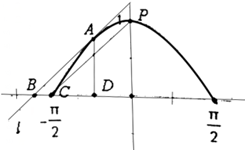 ֱ��l�뺯��y=cosx��x��[-$\frac{��}{2}$��$\frac{��}{2}$]��ͼ�������ڵ�A����l��CP��C��-$\frac{��}{2}$��0����PΪͼ��ļ�ֵ�㣬l��x�ύ��ΪB�����е�A��AD��x�ᣬ����ΪD����$\overrightarrow{BA}•\overrightarrow{BD}$=$\frac{{��}^{2}-4}{4}$��
ֱ��l�뺯��y=cosx��x��[-$\frac{��}{2}$��$\frac{��}{2}$]��ͼ�������ڵ�A����l��CP��C��-$\frac{��}{2}$��0����PΪͼ��ļ�ֵ�㣬l��x�ύ��ΪB�����е�A��AD��x�ᣬ����ΪD����$\overrightarrow{BA}•\overrightarrow{BD}$=$\frac{{��}^{2}-4}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
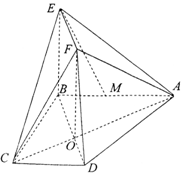 ��ͼ��ʾ������ABCD�����Խ���AC��BD�Ľ���ΪO��AB=2CD���ı���OBEFΪ���Σ�MΪ�߶�AB��һ�㣬AM=2MB��
��ͼ��ʾ������ABCD�����Խ���AC��BD�Ľ���ΪO��AB=2CD���ı���OBEFΪ���Σ�MΪ�߶�AB��һ�㣬AM=2MB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $f��\frac{��}{3}����\sqrt{3}f��\frac{��}{6}��$ | B�� | $f��\frac{��}{6}����\sqrt{2}f��\frac{��}{4}��$ | C�� | $f��\frac{��}{3}����f��\frac{��}{4}��$ | D�� | $f��\frac{��}{4}����\sqrt{3}f��\frac{��}{3}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [1��e] | B�� | $��{1+\frac{1}{e}��e}]$ | C�� | ��0��e] | D�� | $[{1+\frac{1}{e}��e}]$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com