
分析 (Ⅰ)由Sn=$\frac{{{n^2}+3n}}{2}$求得首项,再由an=Sn-Sn-1(n≥2)求得an,验证首项后可得数列{an}的通项公式.设出等比数列的公比,由已知列式求得首项和公比,代入等比数列的通项公式可得{bn}的通项公式;
(Ⅱ)由cn是an与bn+1的等比中项,可得数列{cn2}的通项,然后利用错位相减法求得数列{cn2}的前n项和Tn.
解答 解:(Ⅰ)由Sn=$\frac{{{n^2}+3n}}{2}$,得a1=S1=2.
当n≥2时,${a}_{n}={S}_{n}-{S}_{n-1}=\frac{{n}^{2}+3n}{2}-\frac{(n-1)^{2}+3(n-1)}{2}$=n+1.
验证n=1上式成立,
∴an=n+1;
设等比数列{bn}的公比为q(q>0),由b1+b3=$\frac{20}{3}$,b2+b4=$\frac{20}{9}$,得
$\left\{\begin{array}{l}{{b}_{1}+{b}_{1}{q}^{2}=\frac{20}{3}}\\{{b}_{1}q+{b}_{1}{q}^{3}=\frac{20}{9}}\end{array}\right.$,解得${b}_{1}=6,q=\frac{1}{3}$.
∴${b}_{n}=6×(\frac{1}{3})^{n-1}=2×(\frac{1}{3})^{n-2}$.
(Ⅱ)∵cn是an与bn+1的等比中项,
∴${{c}_{n}}^{2}=2(n+1)•(\frac{1}{3})^{n-1}$.
令Rn=2×$(\frac{1}{3})^{0}+3×(\frac{1}{3})^{1}+4×(\frac{1}{3})^{2}+…+n×(\frac{1}{3})^{n-2}$$+(n+1)×(\frac{1}{3})^{n-1}$.
则$\frac{1}{3}{R}_{n}=2×(\frac{1}{3})^{1}+3×(\frac{1}{3})^{2}+…+n×(\frac{1}{3})^{n-1}+(n+1)×(\frac{1}{3})^{n}$.
∴$\frac{2}{3}{R}_{n}=2+\frac{1}{3}+(\frac{1}{3})^{2}+…+(\frac{1}{3})^{n-1}-(n+1)×(\frac{1}{3})^{n}$=$2+\frac{\frac{1}{3}(1-\frac{1}{{3}^{n-1}})}{1-\frac{1}{3}}-(n+1)×(\frac{1}{3})^{n}$
=$\frac{5}{2}-(n+\frac{5}{2})×\frac{1}{{3}^{n}}$.
∴${R}_{n}=\frac{15}{4}-(\frac{3}{2}n+\frac{15}{4})×\frac{1}{{3}^{n}}$,
则Tn=$2{R}_{n}=\frac{15}{2}-(3n+\frac{15}{2})×\frac{1}{{3}^{n}}$.
点评 本题考查等差数列和等比数列的通项公式,考查错位相减法求数列的前n项和,是中档题.


科目:高中数学 来源: 题型:解答题
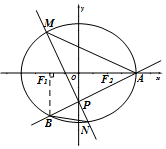 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2,过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2,过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧面PDC⊥底面ABCD,△PDC是等边三角形,AB=AD=$\frac{1}{2}$CD=1,点E,F,G分别是棱PD,PC,BC的中点.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧面PDC⊥底面ABCD,△PDC是等边三角形,AB=AD=$\frac{1}{2}$CD=1,点E,F,G分别是棱PD,PC,BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com