
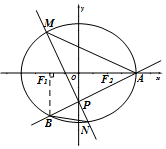
 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2,过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2,过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1.分析 (Ⅰ)当$k=\frac{1}{2}$时,BF1⊥x轴,求出$B(-c,-\frac{b^2}{a})$,列出方程组,求出a,b即可得到椭圆的标准方程.
(Ⅱ)通过民间的比推出$\overrightarrow{PM}=-3\overrightarrow{PN}$.设M(x1,y1),N(x2,y2),设MN方程为y=kx-1,联立直线与椭圆方程,利用韦达定理转化情况直线的斜率,求出直线方程.
解答 解:(Ⅰ)当$k=\frac{1}{2}$时,BF1⊥x轴,得到点$B(-c,-\frac{b^2}{a})$,
所以$\left\{\begin{array}{l}a=2\\ \frac{b^2}{a(a+c)}=\frac{1}{2}\\{a^2}={b^2}+{c^2}\end{array}\right.⇒\left\{\begin{array}{l}a=2\\ b=\sqrt{3}\\ c=1\end{array}\right.$,所以椭圆C的方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(Ⅱ)因为$\frac{{{S_{△PAM}}}}{{{S_{△PBN}}}}=\frac{{\frac{1}{2}PA•PM•sin∠APM}}{{\frac{1}{2}PB•PN•sin∠BPN}}=\frac{2•PM}{1•PN}=\frac{6}{1}⇒\frac{PM}{PN}=3$,所以$\overrightarrow{PM}=-3\overrightarrow{PN}$.
设M(x1,y1),N(x2,y2),则$\overrightarrow{PM}=({x_1},{y_1}+1),\overrightarrow{PN}=({x_2},{y_2}+1)$,有$\left\{\begin{array}{l}{x_1}=-3{x_2}\\{y_1}+1=-3({y_2}+1)\end{array}\right.$.
由(Ⅰ)可知P(0,-1),设MN方程为y=kx-1,
联解方程$\left\{\begin{array}{l}y=kx-1\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$得:(4k2+3)x2-8kx-8=0.
由韦达定理可得$\left\{\begin{array}{l}{x_1}+{x_2}=\frac{8k}{{4{k^2}+3}}\\{x_1}•{x_2}=\frac{-8}{{4{k^2}+3}}\end{array}\right.$,将x1=-3x2代入可得$\left\{\begin{array}{l}-2{x_2}=\frac{8k}{{4{k^2}+3}}\\ 3x_2^2=\frac{8}{{4{k^2}+3}}\end{array}\right.$,
即$3{(\frac{-4k}{{4{k^2}+3}})^2}=\frac{8}{{4{k^2}+3}}$.
所以${k^2}=\frac{3}{2}⇒k=±\frac{{\sqrt{6}}}{2}$,即直线l2的方程为$y=±\frac{{\sqrt{6}}}{2}x-1$.
点评 本题考查直线与椭圆的位置关系的应用,椭圆方程的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{{2\sqrt{6}}}{5}$ | D. | $\frac{{\sqrt{3}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(0,0,0),(1,0,1),(0,1,1),($\frac{1}{2}$,1,0),绘制该四面体三视图时,按照如图所示的方向画正视图,则得到左视图可以为( )
一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(0,0,0),(1,0,1),(0,1,1),($\frac{1}{2}$,1,0),绘制该四面体三视图时,按照如图所示的方向画正视图,则得到左视图可以为( )| A. | 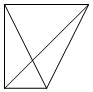 | B. | 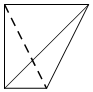 | C. | 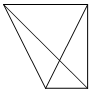 | D. | 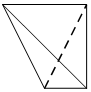 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
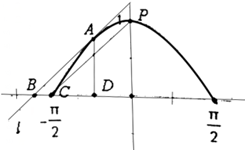 直线l与函数y=cosx(x∈[-$\frac{π}{2}$,$\frac{π}{2}$])图象相切于点A,且l∥CP,C(-$\frac{π}{2}$,0),P为图象的极值点,l与x轴交点为B,过切点A作AD⊥x轴,垂足为D,则$\overrightarrow{BA}•\overrightarrow{BD}$=$\frac{{π}^{2}-4}{4}$.
直线l与函数y=cosx(x∈[-$\frac{π}{2}$,$\frac{π}{2}$])图象相切于点A,且l∥CP,C(-$\frac{π}{2}$,0),P为图象的极值点,l与x轴交点为B,过切点A作AD⊥x轴,垂足为D,则$\overrightarrow{BA}•\overrightarrow{BD}$=$\frac{{π}^{2}-4}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
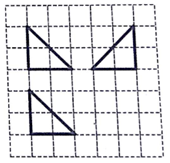 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的各个顶点在某一个球面上,则该球的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的各个顶点在某一个球面上,则该球的表面积为( )| A. | $4\sqrt{3}π$ | B. | 12π | C. | 48π | D. | $32\sqrt{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
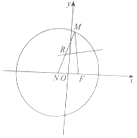 已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.
已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com