
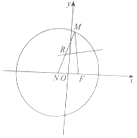
 已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.
已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.分析 (1)利用椭圆的定义,求曲线E的方程;
(2)假设存在直线l使A,F,Q是线段PB的四等分点,则|AF|=$\frac{1}{2}$|FB|.求出直线方程,再进行验证,即可得出结论.
解答 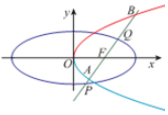 解:(1)由题意,|RM|=|RF|,
解:(1)由题意,|RM|=|RF|,
∴|RF|+|RN|=|RM|+|RN|=|MN|=4>|NF|,
∴R的轨迹是以N,F为焦点的椭圆,a=2,c=1,b=$\sqrt{3}$,
∴曲线E的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1;
(2)抛物线C的顶点在坐标原点,F为其焦点,抛物线的方程为y2=4x,
假设存在直线l使A,F,Q是线段PB的四等分点,则|AF|=$\frac{1}{2}$|FB|.
直线l斜率显然垂直,设方程为y=k(x-1)(k≠0),
设A(x1,y1),B(x2,y2),则直线代入抛物线方程,整理可得ky2-4y-4k=0,
∴y1+y2=$\frac{4}{k}$①,y1y2=-4,②
∵|AF|=$\frac{1}{2}$|FB|,∴$\frac{{y}_{2}}{{y}_{1}}$=-2③,
∴由①②③解得k=±2$\sqrt{2}$.
k=2$\sqrt{2}$时,直线l的方程为y=2$\sqrt{2}$(x-1),解得A($\frac{1}{2}$,-$\sqrt{2}$),B(2,2$\sqrt{2}$).
直线与椭圆方程联立解得P($\frac{2}{5}$,-$\frac{6\sqrt{2}}{5}$),A($\frac{10}{7}$,$\frac{6\sqrt{2}}{7}$),
∵yB≠2yQ,∴Q不是FB的中点,即A,F,Q不是线段PB的四等分点,
同理可得k=-2$\sqrt{2}$时,A,F,Q不是线段PB的四等分点,
∴不存在直线l使A,F,Q是线段PB的四等分点.
点评 本题考查点的轨迹方程的求法,考查直线与椭圆位置关系的运用,考查学生的计算能力,考查反证法,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
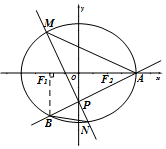 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2,过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2,过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
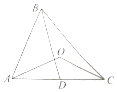 如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$.
如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧面PDC⊥底面ABCD,△PDC是等边三角形,AB=AD=$\frac{1}{2}$CD=1,点E,F,G分别是棱PD,PC,BC的中点.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧面PDC⊥底面ABCD,△PDC是等边三角形,AB=AD=$\frac{1}{2}$CD=1,点E,F,G分别是棱PD,PC,BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com