
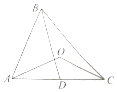
 如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$.
如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$.分析 (Ⅰ)由圆的性质可知∠AOC=2∠ABC.2cos2∠ABC-1=-$\frac{3}{4}$.解得cos∠ABC.
(Ⅱ)过点C作CE∥BA,与DB的延长线交于点E,连接AE在△BCE中,由余弦定理解得CE=2,AB=2.可得△ABC的面积s=$\frac{1}{2}×2×2\sqrt{2}×\frac{\sqrt{14}}{4}=\sqrt{7}$.
解答 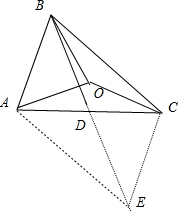 解:(Ⅰ)由圆的性质可知∠AOC=2∠ABC.
解:(Ⅰ)由圆的性质可知∠AOC=2∠ABC.
∵cos∠AOC=-$\frac{3}{4}$.∴2cos2∠ABC-1=-$\frac{3}{4}$.
解得cos∠ABC=$\frac{\sqrt{2}}{4}$.
(Ⅱ)过点C作CE∥BA,与DB的延长线交于点E,连接AE
又∵D为AC边的中点,所以D为平行四边形ABCE对角线的交点.
∴cos∠BCE=-cos∠ABC=-$\frac{\sqrt{2}}{4}$.
在△BCE中,BC=2$\sqrt{2}$,BE=2DB=4,cos∠BCE=-$\frac{\sqrt{2}}{4}$.
由余弦定理得BE2=BC2+CE2-2×BC×CE×cos∠BCE,
解得CE=2,∴AB=2.
∵cos∠ABC=$\frac{\sqrt{2}}{4}$,∴$sin∠ABC=\frac{\sqrt{14}}{4}$
∴△ABC的面积s=$\frac{1}{2}×2×2\sqrt{2}×\frac{\sqrt{14}}{4}=\sqrt{7}$.
点评 本题考查了正余弦定理的应用,三角形的面积计算,添加辅助线对条件进行转化,属于中档题.


科目:高中数学 来源: 题型:选择题
 一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(0,0,0),(1,0,1),(0,1,1),($\frac{1}{2}$,1,0),绘制该四面体三视图时,按照如图所示的方向画正视图,则得到左视图可以为( )
一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(0,0,0),(1,0,1),(0,1,1),($\frac{1}{2}$,1,0),绘制该四面体三视图时,按照如图所示的方向画正视图,则得到左视图可以为( )| A. | 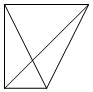 | B. | 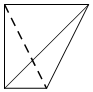 | C. | 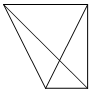 | D. | 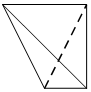 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+2)2+y2=16 | B. | (x+2)2+y2=20 | C. | (x+2)2+y2=25 | D. | (x+2)2+y2=36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
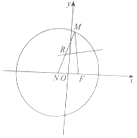 已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.
已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|-1≤a≤1} | B. | {a|a≤-1} | C. | {a|a≤-1或a≥1} | D. | {a|a≥1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com