
| A. | (x+2)2+y2=16 | B. | (x+2)2+y2=20 | C. | (x+2)2+y2=25 | D. | (x+2)2+y2=36 |
分析 根据题意,将直线的方程变形可得m(3x-2y)+(x+y-5)=0,分析可得其定点M(2,3),进而分析可得满足题意的圆是以P为圆心,半径为MP的圆,求出MP的长,将其代入圆的标准方程计算可得答案.
解答 解:根据题意,设圆心为P,则点P的坐标为(-2,0)
对于直线(3m+1)x+(1-2m)y-5=0,变形可得m(3x-2y)+(x+y-5)=0
即直线过定点M(2,3),
在以点(-2,0)为圆心且与直线(3m+1)x+(1-2m)y-5=0,
面积最大的圆的半径r长为MP,
则r2=MP2=25,
则其标准方程为(x+2)2+y2=25;
故选C.
点评 本题考查直线与圆的位置关系,关键是分析出直线(3m+1)x+(1-2m)y-5=0过的定点坐标.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
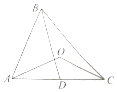 如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$.
如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -i | C. | -1 | D. | i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
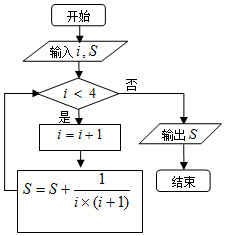
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| A类 | B类 | C类 | |
| 男生 | 18 | x | 3 |
| 女生 | 10 | 8 | y |
| 男生 | 女生 | 总计 | |
| A类 | |||
| B类和C类 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com