
分析 (Ⅰ)设动圆P的半径为r,由圆与圆的位置关系分析可得|PF2|+|PF1|=4>|F1F2|,由椭圆的定义分析可得轨迹C是以F1,F2为焦点的椭圆,由椭圆的定义分析可得轨迹C的方程,即可得答案;
(Ⅱ)设A(x1,y1),B(x2,y2),联立直线l与椭圆C的方程可得(3+4k2)x2-16kx+4=0,利用根与系数的关系可以表示|AB|的值,进而可以表示△OAB面积,由基本不等式的性质分析可得答案.
解答 解:(Ⅰ)设动圆P的半径为r,
依题意有|PF1|=3-r,|PF2|=1+r,|PF2|+|PF1|=4>|F1F2|.
所以轨迹C是以F1,F2为焦点的椭圆,
且c=1,a=2,所以$b=\sqrt{3}$,
当P点坐标为椭圆右顶点时,r=0不符合题意,舍去.
所以轨迹C的方程$\frac{x^2}{4}+\frac{y^2}{3}=1({x≠2})$.
(Ⅱ)设A(x1,y1),B(x2,y2),
联立直线l与椭圆C的方程$\left\{\begin{array}{l}y=kx-2\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$,可得(3+4k2)x2-16kx+4=0,
${x_1}+{x_2}=\frac{16k}{{3+4{k^2}}},{x_1}{x_2}=\frac{4}{{3+4{k^2}}}$,
△=16(12k2-3)>0,得${k^2}>\frac{1}{4}$,
设原点到直线AB的距离为$d=\frac{2}{{\sqrt{1+{k^2}}}}$,
$|{AB}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=\sqrt{1+{k^2}}\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}=\sqrt{1+{k^2}}\frac{{4\sqrt{3}\sqrt{4{k^2}-1}}}{{3+4{k^2}}}$,
${S_{△AOB}}=\frac{1}{2}|{AB}|•d=\frac{{4\sqrt{3}\sqrt{4{k^2}-1}}}{{3+4{k^2}}}$,
令$\sqrt{4{k^2}-1}=t,({t>0})$,则4k2=1+t2,
${S_{△AOB}}=\frac{{4\sqrt{3}t}}{{{t^2}+4}}=\frac{{4\sqrt{3}}}{{t+\frac{4}{t}}}≤\frac{{4\sqrt{3}}}{{2\sqrt{t•\frac{4}{t}}}}=\sqrt{3}$,当且仅当t=2时,等号成立,
即当$k=±\frac{{\sqrt{5}}}{2}$时,△OAB面积取得最大值$\sqrt{3}$,此时直线方程为$y=±\frac{{\sqrt{5}}}{2}x-2$.
点评 本题考查椭圆的几何性质,涉及椭圆与直线的位置关系,关键是求出椭圆的标准方程.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(\frac{π}{3})<\sqrt{3}f(\frac{π}{6})$ | B. | $f(\frac{π}{6})<\sqrt{2}f(\frac{π}{4})$ | C. | $f(\frac{π}{3})<f(\frac{π}{4})$ | D. | $f(\frac{π}{4})<\sqrt{3}f(\frac{π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
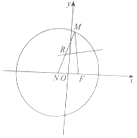 已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.
已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com