
分析 (1)由an=n>0,可知数列{Tn}为递增数列,分别计算T17,T18,即可得出.
(2)利用数列递推关系、等比数列的通项公式即可得出.
(3)由题意b1=T2-2T1=a2a3-a1a2,当n≥2,n∈N*时,bn=Tn+1+Tn-1-2Tn=an+1an+2-anan+1,可得:对任意n∈N*,都有bn=an+1an+2-anan+1. 利用等差数列的定义通项公式分别证明:必要性与充分性即可得出.
解答 (1)解:由an=n>0,可知数列{Tn}为递增数列,…(2分)
计算得T17=1938<2017,T18=2280>2017,
所以不存在k∈N*,使得Tk=2017; …(4分)
(2)解:由${T_n}={6^n}-1$,可以得到当n≥2,n∈N*时,${a_n}{a_{n+1}}={T_n}-{T_{n-1}}=({6^n}-1)-({6^{n-1}}-1)=5•{6^{n-1}}$,…(6分)
又因为a1a2=T1=5,
所以${a_n}{a_{n+1}}=5•{6^{n-1}},n∈{N^*}$,进而得到${a_{n+1}}{a_{n+2}}=5•{6^n},n∈{N^*}$,
两式相除得$\frac{{{a_{n+2}}}}{a_n}=6,n∈{N^*}$,
所以数列{a2k-1},{a2k}均为公比为6的等比数列,…(8分)
由a1=3,得${a_2}=\frac{5}{3}$,
所以an=$\left\{\begin{array}{l}{3•{6}^{\frac{n-1}{2}},n=2k-1}\\{\frac{5}{3}•{6}^{\frac{n-2}{2}},n=2k}\end{array}\right.$,k∈N*.…(10分)
(3)证明:由题意b1=T2-2T1=a2a3-a1a2,
当n≥2,n∈N*时,bn=Tn+1+Tn-1-2Tn=an+1an+2-anan+1,
因此,对任意n∈N*,都有bn=an+1an+2-anan+1. …(12分)
必要性(⇒):若{an}为等差数列,不妨设an=bn+c,其中b,c为常数,
显然a2-a1=a3-a2=a4-a3,
由于bn=an+1an+2-anan+1=${a_{n+1}}({a_{n+2}}-{a_n})=2{b^2}n+2{b^2}+2bc$,
所以对于n∈N*,${b_{n+1}}-{b_n}=2{b^2}$为常数,
故{bn}为等差数列; …(14分)
充分性(?):由于{an}的前4项为等差数列,不妨设公差为d
当n≤k+3(k=1)时,有a4=a1+3d,a3=a1+2d,a2=a1+d成立.…(15分)
假设n≤k+3(k>1,k∈N*)时{an}为等差数列,
即ak+3=ak+3d,ak+2=ak+2d,ak+1=ak+d…(16分)
当n=k+4(k>1,k∈N*)时,由{bn}为等差数列,得bk+2+bk=2bk+1,
即:(ak+3ak+4-ak+2ak+3)+(ak+1ak+2-akak+1)=2(ak+2ak+3-ak+1ak+2),
所以${a_{k+4}}=\frac{{3{a_{k+2}}{a_{k+3}}-3{a_{k+1}}{a_{k+2}}+{a_k}{a_{k+1}}}}{{{a_{k+3}}}}$…(17分)
=$\frac{{3({a_k}+2d)({a_k}+3d)-3({a_k}+d)({a_k}+2d)+{a_k}({a_k}+d)}}{{{a_k}+3d}}$=$\frac{{{a_k}^2+7{a_k}d+12{d^2}}}{{{a_k}+3d}}={a_k}+4d$,
因此ak+4-ak+3=d,
综上所述:数列{an}为等差数列. …(18分)
点评 本题考查了数列递推关系、等差数列的定义通项公式、分类讨论方法、简易逻辑的判定方法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
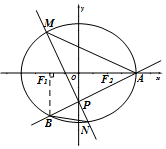 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2,过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2,过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com